题目内容
已知函数f(n)=k,(n∈N*),k是
小数点后第n位数字,
=1.414213562…,则
=( )
| 2 |
| 2 |
| ||
| 2013个f |
| A、1 | B、2 | C、4 | D、6 |
考点:函数的值
专题:函数的性质及应用
分析:利用函数的性质求解.
解答:
解:∵函数f(n)=k,(n∈N*),
k是
小数点后第n位数字,
=1.414213562…,
∴f(8)=6,
f[f(8)]=f(6)=3,
f{f[f(8)]}=f(3)=4,
f{f{f[f(8)]}}=f(4)=2,
f{f{f{f[f(8)]}}=f(2)=1,
f{f{f{f{f[f(8)]}}=f(1)=4,
∵2013=2+670×3+1,
∴
=f(1)=4,
故选:C.
k是
| 2 |
| 2 |
∴f(8)=6,
f[f(8)]=f(6)=3,
f{f[f(8)]}=f(3)=4,
f{f{f[f(8)]}}=f(4)=2,
f{f{f{f[f(8)]}}=f(2)=1,
f{f{f{f{f[f(8)]}}=f(1)=4,
∵2013=2+670×3+1,
∴
| ||
| 2013个f |
故选:C.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
已知等比数列{an}的前n项积为Πn,若a2•a4•a6=8,则Π7等于( )
| A、512 | B、256 |
| C、81 | D、128 |
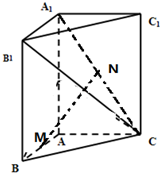 如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.
如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.