题目内容
已知函数f(x)=
sin2x-cos2x-
,x∈R.
(1)求函数f(x)的最小正周期及单调递增区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,若f(A)=0且a=4,b+c=5.求△ABC的面积.
| ||
| 2 |
| 1 |
| 2 |
(1)求函数f(x)的最小正周期及单调递增区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,若f(A)=0且a=4,b+c=5.求△ABC的面积.
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的求值,三角函数的图像与性质,解三角形
分析:(1)首先利用三角恒等变换把函数关系式转化成正弦型函数,进一步求出最小正周期和单调区间.
(2)利用(1)的结论,先根据角A的范围,利用f(A)=0先求出A的值,进一步利用余弦定理求出
bc=3,再利用三角形的面积公式求出结果.
(2)利用(1)的结论,先根据角A的范围,利用f(A)=0先求出A的值,进一步利用余弦定理求出
bc=3,再利用三角形的面积公式求出结果.
解答:
解:(1)函数f(x)=
sin2x-cos2x-
=sin(2x-
)-1,
则:函数的最小正周期:T=
=π
令:-
+2kπ≤2x-
≤2kπ+
(k∈Z)
解得:-
+kπ≤x≤kπ+
(k∈Z)
则:函数f(x)的单调递增区间为:[-
+kπ,kπ+
](k∈Z)
(2)由(1)得:f(x)=sin(2x-
)-1,
则:f(A)=sin(2A-
)-1=0
由于:0<A<π
所以:-
<2A-
<
2A-
=
解得:A=
由余弦定理得:a2=b2+c2-2bccosA
解得:bc=3
S△ABC=
bcsinA=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
则:函数的最小正周期:T=
| 2π |
| 2 |
令:-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得:-
| π |
| 6 |
| π |
| 3 |
则:函数f(x)的单调递增区间为:[-
| π |
| 6 |
| π |
| 3 |
(2)由(1)得:f(x)=sin(2x-
| π |
| 6 |
则:f(A)=sin(2A-
| π |
| 6 |
由于:0<A<π
所以:-
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
2A-
| π |
| 6 |
| π |
| 2 |
解得:A=
| π |
| 3 |
由余弦定理得:a2=b2+c2-2bccosA
解得:bc=3
S△ABC=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
点评:本题考查的知识点:三角函数关系式的恒等变换,正弦型函数的最小正周期和单调区间的确定,利用角的范围确定角的大小,余弦定理得应用,三角形面积的应用.

练习册系列答案
相关题目
已知函数f(x)=
,则f(
)=( )
|
| 1 |
| 9 |
| A、0 | B、1 | C、3 | D、-2 |
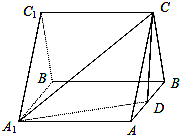 如图,三棱柱ABCA1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D为棱AB的中点.
如图,三棱柱ABCA1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D为棱AB的中点.