题目内容
已知直线l:2x+y+4=0与圆C:x2+y2+2x-4y+1=0的两个交点分别为A,B.
(1)求A,B的坐标;
(2)点D在x轴上,使三角形ABD为等腰三角形,求点D的坐标.
(1)求A,B的坐标;
(2)点D在x轴上,使三角形ABD为等腰三角形,求点D的坐标.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)利用方程组可以解得交点A,B的坐标;
(2)因为不能确定哪个角是直角,所以需分类讨论,然后利用垂直、模长相等列方程(组).
(2)因为不能确定哪个角是直角,所以需分类讨论,然后利用垂直、模长相等列方程(组).
解答:
解:(1)由
可得两交点的坐标分别为A (-
,
),B (-3,2).
(2)①当DA=DB时,易得直线l的斜率为-2,线段AB的垂直平分线的斜率为
,中点为 (-
,
),
所以线段AB的垂直平分线的方程为x-2y+5=0.
所以点D的坐标为(-5,0).
②当DA=BA时,以A 为圆心,AB为半径的圆A的方程为(x+
)2+(y-
) 2=
.
圆A与x轴的交点为(-
+
,0)和(-
-
,0).
③当BA=BD时,以B为圆心,AB为半径的圆与x轴无交点.
所以,点D的坐标为 (-5,0)或(-
+
,0)或(-
-
,0).
|
| 11 |
| 5 |
| 2 |
| 5 |
(2)①当DA=DB时,易得直线l的斜率为-2,线段AB的垂直平分线的斜率为
| 1 |
| 2 |
| 13 |
| 5 |
| 6 |
| 5 |
所以线段AB的垂直平分线的方程为x-2y+5=0.
所以点D的坐标为(-5,0).
②当DA=BA时,以A 为圆心,AB为半径的圆A的方程为(x+
| 11 |
| 5 |
| 2 |
| 5 |
| 16 |
| 5 |
圆A与x轴的交点为(-
| 11 |
| 5 |
2
| ||
| 5 |
| 11 |
| 5 |
2
| ||
| 5 |
③当BA=BD时,以B为圆心,AB为半径的圆与x轴无交点.
所以,点D的坐标为 (-5,0)或(-
| 11 |
| 5 |
2
| ||
| 5 |
| 11 |
| 5 |
2
| ||
| 5 |
点评:本题考查了直线、圆的交点问题,即利用它们的方程来研究交点问题,结合垂直、距离公式构造方程组求解.

练习册系列答案
相关题目
已知直线l:2x+y+4=0,圆C:x2+y2+2x-4y+1=0.
(1)直线m与直线l平行,且与圆C相切,求m的方程;
(2)设直线l和圆C的两个交点分别为A,B,求过A,B的圆中面积最小的圆的方程.
(1)直线m与直线l平行,且与圆C相切,求m的方程;
(2)设直线l和圆C的两个交点分别为A,B,求过A,B的圆中面积最小的圆的方程.
已知y=f(x)为定义在R上的函数,则“存在X0∈R,使得f2(-x0)≠f2(x0)”是“f(x)为非奇非偶函数”的( )
| A、充分非必要 |
| B、必要非充分 |
| C、充分必要 |
| D、既不充分也不必要 |
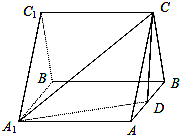 如图,三棱柱ABCA1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D为棱AB的中点.
如图,三棱柱ABCA1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D为棱AB的中点.