题目内容
如图，PA﹑PB是⊙O的切线，切点分别为A﹑B，线段OP交⊙O于点C，若PA=8，PC=4，求AB的长．
考点：与圆有关的比例线段
专题：立体几何
分析：（延长PO交⊙O于D，连结AO，BO，AB交OP于点E．由切割线定理得PA2=PC•PD，由此结合已知条件能求出AB的长．
解答：
（本小题满分12分）
解：如图，延长PO交⊙O于D，连结AO，BO，AB交OP于点E．
因为PA与⊙O相切，
所以PA2=PC•PD…（3分）
设⊙O的半径为R，因为PA=8，PC=4
所以82=4（2R+4），解得R=6…（6分）
因为PA，PB与⊙O均相切，所以PA=PB
又OA=OB，所以OP是线段AB的垂直平分线
即AB⊥OP，且AB=2AE．
在Rt△AOP中，AE=
=
…（9分）
所以AB=
…（12分）
（本小题满分12分）解：如图，延长PO交⊙O于D，连结AO，BO，AB交OP于点E．
因为PA与⊙O相切，
所以PA2=PC•PD…（3分）
设⊙O的半径为R，因为PA=8，PC=4
所以82=4（2R+4），解得R=6…（6分）
因为PA，PB与⊙O均相切，所以PA=PB
又OA=OB，所以OP是线段AB的垂直平分线
即AB⊥OP，且AB=2AE．
在Rt△AOP中，AE=
| OA•PA |
| OP |
| 24 |
| 5 |
所以AB=
| 48 |
| 5 |
点评：本题考查线段长的求法，是中档题，解题时要认真审题，注意切割线定理的合理运用．
练习册系列答案
导学教程高中新课标系列答案
相关题目
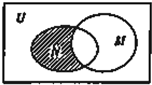设全集U为实数集R，M={x|x＞2}，N={x|x＜4}，则图中阴影部分所表示的集合是（ ）| A、{x|x≤2} |
| B、{x|x≥4} |
| C、{x|x＜2} |
| D、{x|2＜x＜4} |
已知A（1，1），B（3，5），则直线AB的垂直平分线为（ ）
| A、x-2y-8=0 |
| B、2x+y+8=0 |
| C、x+2y-8=0 |
| D、2x-y-8=0 |
已知椭圆C1：
+
=1的左焦点为F，点P为椭圆上一动点，过点P向以F为圆心，1为半径的圆作切线PM、PN，其中切点为M、N，则四边形PMFN面积的最大值为（ ）
| x2 |
| 16 |
| y2 |
| 15 |
A、2
| ||
B、
| ||
C、
| ||
| D、5 |
等差数列{an}中，前n项和为Sn，若S16-S5=165则a9+a8+a16=（ ）
| A、90 | B、-80 | C、75 | D、45 |
2013年12月26日上午，日本首相安倍晋三参拜了靖国神社．这是安倍两次出任首相以来首次参拜，引起周边国家的强烈谴责，我军为了加强防范外敌入侵加强军事演习．在某次军事演习中红方为了准确分析战场形势，在两个相距为