题目内容
等差数列{an}中，前n项和为Sn，若S16-S5=165则a9+a8+a16=（ ）
| A、90 | B、-80 | C、75 | D、45 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用等差数列的求和公式，可得a1+10d=15，再利用等差数列的通项公式，即可得出结论．
解答：
解：∵等差数列{an}中，前n项和为Sn，S16-S5=165，
∴16a1+120d-5a1-10d=165，
∴a1+10d=15，
∴a9+a8+a16=a1+8d+a1+7d+a1+15d=45．
故选：D．
∴16a1+120d-5a1-10d=165，
∴a1+10d=15，
∴a9+a8+a16=a1+8d+a1+7d+a1+15d=45．
故选：D．
点评：本题考查等差数列的通项、求和公式，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
在△ABC中，a=
，b=
，A=
，则（ ）
| 5 |
| 15 |
| π |
| 6 |
A、c=2
| ||||
B、c=
| ||||
C、c=2
| ||||
| D、以上都不正确 |
命题“?x＞0，x2+ax+1＜0”的否定是（ ）
| A、?x≤0，x2+ax+1＜0 |
| B、?x＞0，x2+ax+1≥0 |
| C、?x＞0，x2+ax+1＜0 |
| D、?x＞0，x2+ax+1≥0 |
设变量x，y满足约束条件
，则z=x2-x+y2的最小值为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、-
|
如果a＞b，给出下列不等式：（1）
＜
；（2）a3＞b3；（3）a2+1＞b2+1；（4）2a＞2b．其中成立的不等式有（ ）
| 1 |
| a |
| 1 |
| b |
| A、（3）（4） |
| B、（2）（3） |
| C、（2）（4） |
| D、（1）（3） |
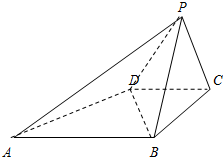如图，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，