题目内容
已知函数f(x)=lnx-λx+λ(λ∈R).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)请问,是否存在实数λ使f(x)≤0在x∈(0,+∞)上恒成立?若存在,请求实数λ的值;若不存在,请说明理由.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)请问,是否存在实数λ使f(x)≤0在x∈(0,+∞)上恒成立?若存在,请求实数λ的值;若不存在,请说明理由.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:综合题,导数的概念及应用
分析:(Ⅰ)求导数,分类讨论,利用导数的正负,可得函数f(x)的单调区间;
(Ⅱ)确定函数的最大值,可得λ-lnλ-1≤0即可,构造新函数,确定函数的单调性,可得函数的最小值,即可得出结论.
(Ⅱ)确定函数的最大值,可得λ-lnλ-1≤0即可,构造新函数,确定函数的单调性,可得函数的最小值,即可得出结论.
解答:
解:(Ⅰ)f/(x)=
-λ=
,(x∈(0,+∞))…(2分)
当λ≤0时,f′(x)>0恒成立,
则函数f(x)在(0,+∞)上单调递增…(4分)
当λ>0时,由f/(x)=
-λ=
>0得0<x<
,
则f(x)在(0,
)上单调递增,在(
,+∞)上单调递减…(6分)
(Ⅱ)存在.…(7分)
由(Ⅰ)得:当λ≤0时,函数f(x)在(0,+∞)上单调递增f(x)≤0显然不成立;
当λ>0时,f(x)在(0,
)上单调递增,在(
,+∞)上单调递减,
∴f(x)max=f(
)=ln
-1+λ=λ-lnλ-1,
只需λ-lnλ-1≤0即可 …(9分)
令g(x)=x-lnx-1
则g/(x)=1-
,
函数g(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
∴g(x)min=g(1)=0,…(10分)
即g(x)≥0对x∈(0,+∞)恒成立,
也就是λ-lnλ-1≥0对λ∈(0,+∞)恒成立,
∴λ-lnλ-1=0解得λ=1,
∴若f(x)≤0在x∈(0,+∞)上恒成立,λ=1. …(12分)
| 1 |
| x |
| 1-λx |
| x |
当λ≤0时,f′(x)>0恒成立,
则函数f(x)在(0,+∞)上单调递增…(4分)
当λ>0时,由f/(x)=
| 1 |
| x |
| 1-λx |
| x |
| 1 |
| λ |
则f(x)在(0,
| 1 |
| λ |
| 1 |
| λ |
(Ⅱ)存在.…(7分)
由(Ⅰ)得:当λ≤0时,函数f(x)在(0,+∞)上单调递增f(x)≤0显然不成立;
当λ>0时,f(x)在(0,
| 1 |
| λ |
| 1 |
| λ |
∴f(x)max=f(
| 1 |
| λ |
| 1 |
| λ |
只需λ-lnλ-1≤0即可 …(9分)
令g(x)=x-lnx-1
则g/(x)=1-
| 1 |
| x |
函数g(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
∴g(x)min=g(1)=0,…(10分)
即g(x)≥0对x∈(0,+∞)恒成立,
也就是λ-lnλ-1≥0对λ∈(0,+∞)恒成立,
∴λ-lnλ-1=0解得λ=1,
∴若f(x)≤0在x∈(0,+∞)上恒成立,λ=1. …(12分)
点评:本题考查函数的单调性,考查 恒成立问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目

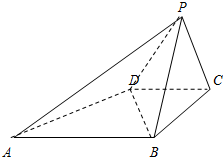 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°, 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,点E为⊙O上一点,
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,点E为⊙O上一点,