题目内容
已知函数f(x)=lnx+
-1.
(1)求函数f(x)的单调区间;
(2)设m∈R,对任意的a∈(-1,1),总存在x0∈[1,e],使得不等式ma-f(x0)<0成立,求实数m的取值范围;
(3)若{an}是首项为1的正项数列,且nan+12-(n+1)an2-an+1an=0,若不等式e(n-1)α≥an对任意的n≥2且n∈N*都成立,求α的取值范围.
| 1 |
| x |
(1)求函数f(x)的单调区间;
(2)设m∈R,对任意的a∈(-1,1),总存在x0∈[1,e],使得不等式ma-f(x0)<0成立,求实数m的取值范围;
(3)若{an}是首项为1的正项数列,且nan+12-(n+1)an2-an+1an=0,若不等式e(n-1)α≥an对任意的n≥2且n∈N*都成立,求α的取值范围.
考点:数列与不等式的综合,利用导数研究函数的单调性
专题:计算题,压轴题,函数的性质及应用,导数的综合应用,等差数列与等比数列
分析:(1)由函数f(x)=lnx+
-1确定函数的定义域并求导,从而求函数f(x)的单调区间;
(2)先由(1)求得0≤f(x0)≤
,从而将对任意的a∈(-1,1),总存在x0∈[1,e],使得不等式ma-f(x0)<0成立化为对任意的a∈(-1,1),ma<
恒成立,从而求实数m的取值范围;
(3)由nan+12-(n+1)an2-an+1an=0可求得an=n,从而化不等式e(n-1)α≥an对任意的n≥2且n∈N*都成立为e(n-1)α≥n对任意的n≥2且n∈N*都成立,注意到当n=2时,eα≥2,则α≥ln2>
;则在α≥ln2>
下讨论即可,
故可判断f(x)=(x-1)α-lnx在[2,+∞)上是增函数,从而可求α的取值范围.
| 1 |
| x |
(2)先由(1)求得0≤f(x0)≤
| 1 |
| e |
| 1 |
| e |
(3)由nan+12-(n+1)an2-an+1an=0可求得an=n,从而化不等式e(n-1)α≥an对任意的n≥2且n∈N*都成立为e(n-1)α≥n对任意的n≥2且n∈N*都成立,注意到当n=2时,eα≥2,则α≥ln2>
| 1 |
| 2 |
| 1 |
| 2 |
故可判断f(x)=(x-1)α-lnx在[2,+∞)上是增函数,从而可求α的取值范围.
解答:
解:(1)∵f(x)=lnx+
-1的定义域为(0,+∞),
且f′(x)=
-
=
,
故函数f(x)的单调减区间为(0,1),单调增区间为(1,+∞);
(2)∵函数f(x)在[1,e]上单调递增,
∴0≤f(x0)≤
,
∴对任意的a∈(-1,1),总存在x0∈[1,e],使得不等式ma-f(x0)<0成立可化为
对任意的a∈(-1,1),ma<
恒成立,
故
,
解得,-
≤m≤
;
(3)∵nan+12-(n+1)an2-an+1an=0,
∴[nan+1-(n+1)an][an+1+an]=0,
又∵{an}是首项为1的正项数列,
∴nan+1-(n+1)an=0,
∴
=
,又∵首项为1,
∴an=n,
则不等式e(n-1)α≥an对任意的n≥2且n∈N*都成立可化为e(n-1)α≥n对任意的n≥2且n∈N*都成立;
则当n=2时,eα≥2,则α≥ln2>
;
e(n-1)α≥n对任意的n≥2且n∈N*都成立可化为(n-1)α-lnn≥0对任意的n≥2且n∈N*都成立;
令f(x)=(x-1)α-lnx,则f′(x)=α-
,
则当x∈[2,+∞)时,f′(x)=α-
>0,
f(x)=(x-1)α-lnx在[2,+∞)上是增函数,
故(n-1)α-lnn≥0对任意的n≥2且n∈N*都成立可化为α-ln2≥0,
故α≥ln2.
综上所述,α≥ln2.
| 1 |
| x |
且f′(x)=
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x2 |
故函数f(x)的单调减区间为(0,1),单调增区间为(1,+∞);
(2)∵函数f(x)在[1,e]上单调递增,
∴0≤f(x0)≤
| 1 |
| e |
∴对任意的a∈(-1,1),总存在x0∈[1,e],使得不等式ma-f(x0)<0成立可化为
对任意的a∈(-1,1),ma<
| 1 |
| e |
故
|
解得,-
| 1 |
| e |
| 1 |
| e |
(3)∵nan+12-(n+1)an2-an+1an=0,
∴[nan+1-(n+1)an][an+1+an]=0,
又∵{an}是首项为1的正项数列,
∴nan+1-(n+1)an=0,
∴
| an+1 |
| an |
| n+1 |
| n |
∴an=n,
则不等式e(n-1)α≥an对任意的n≥2且n∈N*都成立可化为e(n-1)α≥n对任意的n≥2且n∈N*都成立;
则当n=2时,eα≥2,则α≥ln2>
| 1 |
| 2 |
e(n-1)α≥n对任意的n≥2且n∈N*都成立可化为(n-1)α-lnn≥0对任意的n≥2且n∈N*都成立;
令f(x)=(x-1)α-lnx,则f′(x)=α-
| 1 |
| x |
则当x∈[2,+∞)时,f′(x)=α-
| 1 |
| x |
f(x)=(x-1)α-lnx在[2,+∞)上是增函数,
故(n-1)α-lnn≥0对任意的n≥2且n∈N*都成立可化为α-ln2≥0,
故α≥ln2.
综上所述,α≥ln2.
点评:本题考查了导数的应用及数列的通项求法,同时考查了恒成立问题及存在性问题的处理,属于难题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
设{an}是公差为正数的等差数列,a1+a2+a3=15,a1a2a3=80,则a6+a7+a8=( )
| A、40 | B、50 | C、60 | D、70 |
设a=log0.53,b=(
)0.2,c=
,则( )
| 1 |
| 3 |
| 3 | 2 |
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<a<c |
如图,下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形序号是( )


| A、①② | B、③④ | C、②③ | D、①④ |
直线y=kx-2与椭圆x2+4y2=80相交于不同的两点P、Q,若PQ的中点横坐标为2,则直线的斜率等于( )
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
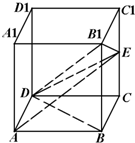 在棱长为2的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.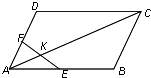 如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于E、F两点,且交其对角线于K,其中,
如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于E、F两点,且交其对角线于K,其中,