题目内容
已知函数f(x)=
x3-x2-3x,求y=f(x)在区间[-3,6]上的最值.
| 1 |
| 3 |
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:由题意,利用导数确定函数的单调性,进而求最值.
解答:
解:∵f(x)=
x3-x2-3x
∴f'(x)=x2-2x-3=(x-3)(x+1)…(3分)
∴f'(x)=x2-2x-3=0解得x=-1或3.…(5分)
x,y,y,取值情况列表如下
…(8分)
∴f(x)极大=f(-1)=
,f(x)极小=f(3)=-9.…(10分)
又f(-3)=-9,f(6)=18,
∴f(x)最大=f(6)=18,f(x)最小=f(3)=f(-3)=-9…(13分)
| 1 |
| 3 |
∴f'(x)=x2-2x-3=(x-3)(x+1)…(3分)
∴f'(x)=x2-2x-3=0解得x=-1或3.…(5分)
x,y,y,取值情况列表如下
| x | (-∞,-1) | -1 | (-1,3) | 3 | (3,+∞) |
| y' | + | 0 | - | 0 | + |
| y | ↑ | 极大值 | ↓ | 极小值 | ↑ |
∴f(x)极大=f(-1)=
| 5 |
| 3 |
又f(-3)=-9,f(6)=18,
∴f(x)最大=f(6)=18,f(x)最小=f(3)=f(-3)=-9…(13分)
点评:本题考查利用导数求闭区间上函数的最值,考查学生的运算能力.

练习册系列答案
相关题目
设全集U={-2,-1,0,1,2},A={-2,-1,0},B={0,1,2}则(∁UA)∩B=( )
| A、{0} |
| B、{-2,-1} |
| C、{0,1,2} |
| D、{1,2} |
函数f(x)=lg(||x2-2x-10|-10|)的零点的个数( )
| A、8 | B、7 | C、6 | D、5 |
钝角△ABC最大边长为4,其余两边长为x,y,以(x,y)为坐标的点所表示的平面区域的面积为( )
| A、4π-8 | ||
| B、4π+8 | ||
| C、4π-6 | ||
D、4π-
|
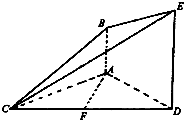 如图,已知DE⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB=2,且F是CD的中点.
如图,已知DE⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB=2,且F是CD的中点.