题目内容
若圆锥的侧面积是底面积的3倍，则其母线与底面所成角的余弦值为 ．
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：根据题意，画出轴截面，结合图形求出母线与底面圆的半径之间的关系，即可得出结论．
解答：
解：根据题意，设圆锥的母线为l，底面圆半径为r，画出轴截面如图所示；
则侧面积是πrl，底面积是πr2；
∴πrl=3πr2，
即l=3r；
∴母线与底面所成角的余弦值为cosθ=
=
．
故答案为：
．
解：根据题意，设圆锥的母线为l，底面圆半径为r，画出轴截面如图所示；则侧面积是πrl，底面积是πr2；
∴πrl=3πr2，
即l=3r；
∴母线与底面所成角的余弦值为cosθ=
| r |
| l |
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题考查了圆锥的侧面积与底面积公式的应用问题，解题时应画出图形，结合图形解答问题，是基础题．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
在复平面内，复数
对应的点位于（ ）
| 1+i |
| (1-i)2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
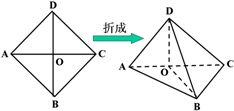如图，以正方形ABCD的对角线AC为折痕，使△ADC和△ABC折成相垂直的两个面，点O为AC的中点．
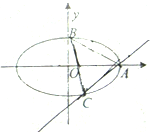已知椭圆