题目内容
13.已知关于x的方程2x2-mx+1=0,$x∈[{\frac{1}{2},4}]$存在两个不同的实根,则实数m的取值范围为( )| A. | (2,3] | B. | $(2\sqrt{2},8\frac{1}{4})$ | C. | $[3,8\frac{1}{4}]$ | D. | $(2\sqrt{2},3]$ |
分析 由题意可得$\left\{\begin{array}{l}{\frac{1}{2}<\frac{m}{4}<4}\\{f(\frac{1}{2})≥0}\\{f(4)≥0}\\{△={m}^{2}-8>0}\end{array}\right.$,解得即可.
解答 解:∵关于x的方程2x2-mx+1=0,$x∈[{\frac{1}{2},4}]$存在两个不同的实根,
∴$\left\{\begin{array}{l}{\frac{1}{2}<\frac{m}{4}<4}\\{f(\frac{1}{2})≥0}\\{f(4)≥0}\\{△={m}^{2}-8>0}\end{array}\right.$,
解得2$\sqrt{2}$<m≤3,
故选:D.
点评 本题考查了二次方程与二次函数之间的关系应用,属于中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
4.在区间(-1,2)中任取一个数x,则使2x>3的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
18.方程3x+4x=6x解的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
2.某几何体的三视图如图所示,则该几何体外接球的表面积为( )
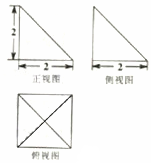

| A. | 4π | B. | 12π | C. | 48π | D. | 6$\sqrt{3}$π |
3.设a=log310,b=log37,则3a-b=( )
| A. | $\frac{10}{49}$ | B. | $\frac{49}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{10}{7}$ |
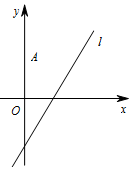 如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=x-1,设圆C的半径为1,圆心在l上.
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=x-1,设圆C的半径为1,圆心在l上.