题目内容
18.方程3x+4x=6x解的个数是( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 方程转化为$\frac{1}{{2}^{x}}$+($\frac{2}{3}$)x-1=0,根据指数函数的单调性得到f(x)$\frac{1}{{2}^{x}}$+($\frac{2}{3}$)x-1为减函数,再根据函数零点存在定理即可判断.
解答 解:方程3x+4x=6x等价于3x+(2x)2=2x•3x,
即为$\frac{1}{{2}^{x}}$+($\frac{2}{3}$)x-1=0,
因为y=($\frac{1}{2}$)x,y=($\frac{2}{3}$)x,均为减函数,
所以f(x)=$\frac{1}{{2}^{x}}$+($\frac{2}{3}$)x-1为减函数,
因为f(1)=$\frac{1}{2}$+$\frac{2}{3}$-1=$\frac{1}{6}$>0,f(2)=$\frac{1}{4}$+$\frac{4}{9}$-1=-$\frac{11}{36}$<0,
所以f(x)在(1,2)上有唯一的零点,
故方程3x+4x=6x解的个数是1个,
故选:B.
点评 本题考查指数函数的性质,得出函数f(x)单调递减是解决问题的关键,属基础题.

练习册系列答案
相关题目
9.抛物线y2=2x的焦点为F,点P在抛物线上,点O为坐标系原点,若|PF|=3,则|PO|等于( )
| A. | $\frac{3\sqrt{5}}{2}$ | B. | 3$\sqrt{3}$ | C. | $\frac{5\sqrt{5}}{2}$ | D. | 4$\sqrt{2}$ |
6.正方体的棱长为2$\sqrt{3}$,顶点都在同一球面上,则该球的表面积为( )
| A. | 36π | B. | 72π | C. | 288π | D. | 144π |
13.已知关于x的方程2x2-mx+1=0,$x∈[{\frac{1}{2},4}]$存在两个不同的实根,则实数m的取值范围为( )
| A. | (2,3] | B. | $(2\sqrt{2},8\frac{1}{4})$ | C. | $[3,8\frac{1}{4}]$ | D. | $(2\sqrt{2},3]$ |
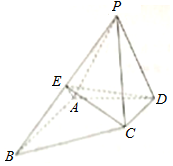 如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点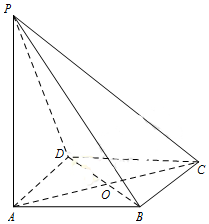 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.