题目内容
化简:cos(π-θ)+tan(π+θ)sin(
-θ)
| π |
| 2 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:原式利用诱导公式化简,整理后再利用两角和与差的正弦函数公式化简即可.
解答:
解:原式=-cosθ+tanθcosθ
=sinθ-cosθ
=
(
sinθ-
cosθ)
=
sin(θ-
).
=sinθ-cosθ
=
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 2 |
| π |
| 4 |
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
函数y=lg(x+1)+
的定义域是( )
| 1-x |
| A、[-1,1] |
| B、(-1,1) |
| C、[-1,1) |
| D、(-1,1] |
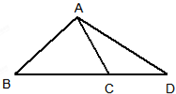 如图,在△ABC中,内角A,B,C的对边分别是a,b,c,且bsinA=acosB,D是BC延长线上的一点,AC=5,AD=7,CD=3.
如图,在△ABC中,内角A,B,C的对边分别是a,b,c,且bsinA=acosB,D是BC延长线上的一点,AC=5,AD=7,CD=3.