题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c,且2
asinB=5c,cosB=
.
(Ⅰ)求角A的大小;
(Ⅱ)设BC边的中点为D,|AD|=
,求△ABC的面积.
| 3 |
| 11 |
| 14 |
(Ⅰ)求角A的大小;
(Ⅱ)设BC边的中点为D,|AD|=
| ||
| 2 |
考点:正弦定理,余弦定理
专题:解三角形
分析:(Ⅰ)利用同角三角函数关系求得sinB的值,利用2
asinB=5c求得a和c的关系,进而利用正弦定理求得转化成角的正弦,利用两角和公式化简整理求得sinA和cosA的关系,求得tanA的值,进而求得A.
(Ⅱ)利用余弦定理求得c,进而求得b,最后根据三角形面积公式求得答案.
| 3 |
(Ⅱ)利用余弦定理求得c,进而求得b,最后根据三角形面积公式求得答案.
解答:
解:( I)在△ABC中,∵cosB=
,
∴sinB=
,
∵2
asinB=5c,
∴2
•a•
=5c
∴3a=7c,
∵
=
,
∴3sinA=7sinC,
∴3sinA=7sin(A+B),
∴3sinA=7sinAcosB+7cosAsinB,即3sinA=7•sinA•
+7cosA
∴-sinA=
cosA,
∴tanA=-
,即A=
.
(Ⅱ)∵AB2+BD2-2AB•BDcosB=
,
又3a=7c,∴BD=
a=
c,
∴c2+(
c)2-2c•
c•
=
,
∴c=3,则a=7,
∴S=
acsinB=
×3×7×
=
.
| 11 |
| 14 |
∴sinB=
5
| ||
| 14 |
∵2
| 3 |
∴2
| 3 |
5
| ||
| 14 |
∴3a=7c,
∵
| a |
| sinA |
| c |
| sinC |
∴3sinA=7sinC,
∴3sinA=7sin(A+B),
∴3sinA=7sinAcosB+7cosAsinB,即3sinA=7•sinA•
| 11 |
| 14 |
5
| ||
| 14 |
∴-sinA=
| 3 |
∴tanA=-
| 3 |
| 2π |
| 3 |
(Ⅱ)∵AB2+BD2-2AB•BDcosB=
| 19 |
| 4 |
又3a=7c,∴BD=
| 1 |
| 2 |
| 7 |
| 6 |
∴c2+(
| 7 |
| 6 |
| 7 |
| 6 |
| 11 |
| 14 |
| 19 |
| 4 |
∴c=3,则a=7,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
5
| ||
| 14 |
15
| ||
| 4 |
点评:本题主要考查了正弦定理和余弦定理的运用.解题的关键就是利用正弦定理和余弦定理完成边角问题的转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图,下列说法错误的是( )
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图,下列说法错误的是( )| A、乙班平均身高高于甲班 | ||
| B、甲班的样本方差为57.2 | ||
C、从乙班这10名同学中随机抽取两名身高不低于173cm的同学,可得身高为176cm的同学被抽中的概率为
| ||
| D、乙班的中位数为178 |
已知集合M={(x,y)|x+y=3},N={(x,y)|x-y=5},那么集合M∩N为( )
| A、x=4,y=-1 |
| B、(4,-1) |
| C、{4,-1} |
| D、{(4,-1)} |
今有5位同学排成一排照相,其中甲、乙两人必须相邻,则不同的排法共有( )
| A、48种 | B、24种 |
| C、8种 | D、20种 |
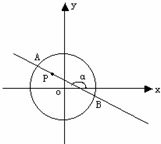 圆x2+y2=8内有一点P(-1,2),AB为过点P且倾斜角为α的弦,
圆x2+y2=8内有一点P(-1,2),AB为过点P且倾斜角为α的弦,