题目内容
求圆心在直线2x+y=0上,且与直线y=-x+1相切于点(2,-1)的圆的方程,并判断点O(0,0),A(1,2-
)与圆的位置关系.
| 2 |
考点:圆的切线方程
专题:直线与圆
分析:设出圆的圆心坐标,利用圆与直线相切,列出方程求出a,得到圆的圆心坐标与半径,求出圆的方程,通过得到圆心的距离与半径比较判断点与圆的位置关系.
解答:
解:∵圆心在直线2x+y=0上,故设圆心为(a,-2a),
又圆与y=-x+1相切点(2,-1),
∴
=
,解得a=1.
∴圆心为C(1,-2),半径r=
=
.
故所求圆的方程为(x-1)2+(y+2)2=2.
∵|OC|=
>
=r,
∴点O在圆C外;
∵A(1,2-
),圆心为C(1,-2),
∴|AC|=
=4-
>
=r,
∴点A在圆外.
又圆与y=-x+1相切点(2,-1),
∴
| |a-2a-1| | ||
|
| (a-2)2+(-2a+1)2 |
∴圆心为C(1,-2),半径r=
| (1-2)2+(-2+1)2 |
| 2 |
故所求圆的方程为(x-1)2+(y+2)2=2.
∵|OC|=
| 5 |
| 2 |
∴点O在圆C外;
∵A(1,2-
| 2 |
∴|AC|=
(1-1)2+(2-
|
| 2 |
| 2 |
∴点A在圆外.
点评:本题考查圆的标准方程的求法,点与圆的位置关系的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
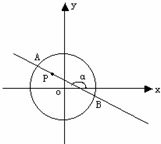 圆x2+y2=8内有一点P(-1,2),AB为过点P且倾斜角为α的弦,
圆x2+y2=8内有一点P(-1,2),AB为过点P且倾斜角为α的弦,