题目内容
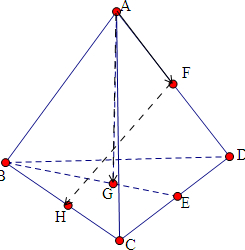
已知在空间四边形ABCD中，G是△BCD的重心，E、F、H分别为边CD、AD和BC的中点，化简下列各表达式，并标出化简结果的向量．
（1）
+
+
（2）
（
+
-
）
（3）
（
+
+
）
（1）
| AG |
| 1 |
| 3 |
| BE |
| 1 |
| 2 |
| CA |
（2）
| 1 |
| 2 |
| AB |
| AC |
| AD |
（3）
| 1 |
| 3 |
| AB |
| AC |
| AD |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的加减运算和向量的共线表示，以及三角形的重心的性质，即可化简得到．
解答：
解：（1）
+
+
=
+
+
+
=
+
+
+
=
+
+
=
+
=
+
+
=
=
，
（2）
（
+
-
）=
-
=
-
=
；
（3）
（
+
+
）=
×2
+
=
（
+
），
在三角形ADH中，
=2
，
则
-
=2（
-
），
即有
=
(2
+
)，
则有
（
+
+
）=
．
解：（1）| AG |
| 1 |
| 3 |
| BE |
| 1 |
| 2 |
| CA |
| AB |
| BG |
| 1 |
| 3 |
| BE |
| 1 |
| 2 |
| CA |
=
| AB |
| 2 |
| 3 |
| BE |
| 1 |
| 3 |
| BE |
| 1 |
| 2 |
| CA |
=
| AB |
| BE |
| 1 |
| 2 |
| CA |
| AE |
| 1 |
| 2 |
| CA |
=
| 1 |
| 2 |
| AC |
| 1 |
| 2 |
| AD |
| 1 |
| 2 |
| CA |
| 1 |
| 2 |
| AD |
| AF |
（2）
| 1 |
| 2 |
| AB |
| AC |
| AD |
| AH |
| 1 |
| 2 |
| AD |
| AH |
| AF |
| FH |
（3）
| 1 |
| 3 |
| AB |
| AC |
| AD |
| 1 |
| 3 |
| AH |
| 1 |
| 3 |
| AD |
=
| 2 |
| 3 |
| AH |
| 1 |
| 2 |
| AD |
在三角形ADH中，
| DG |
| GH |
则
| AG |
| AD |
| AH |
| AG |
即有
| AG |
| 1 |
| 3 |
| AH |
| AD |
则有
| 1 |
| 3 |
| AB |
| AC |
| AD |
| AG |
点评：本题考查向量的加减运算和向量共线的表示，考查运算能力，属于中档题和易错题．
练习册系列答案
相关题目
已知抛物线C：y2=4x，直线l过定点M（a，0），a＞0且与抛物线交于A、B两点，O为坐标原点，若∠AOB为锐角，则实数a的取值范围是（ ）
| A、0＜a＜4 | B、a＞4 |
| C、a≥2 | D、0＜a＜2 |
设
，
，
为单位向量，
，
的夹角为60°，则（
+
）•
的最大值为（ ）
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
A、
| ||
B、
| ||
| C、3 | ||
| D、2 |
椭圆：
+
=1（a＞b＞0）上存在点P使
•
＜0，则离心率e∈（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
A、（0，
| ||||
B、（0，
| ||||
C、（
| ||||
D、（
|
已知A（-2，0），B（2，0）为坐标平面上两个定点，动点M在x轴上的射影为N，且满足|MN|2=4|AN|•|BN|．
如图，正方体的底面与正四面体的底面在同一平面α上，且棱AB所在的直线与棱CD所在的直线互相平行，正方体的六个面所在的平面与直线CE、EF相交的平面个数分别记为m，n，那么m=