题目内容

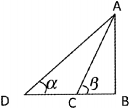如图D，C，B三点在地面同一直线上，DC=a，从C，D两点测得A点的仰角分别为β，α（α＜β），则A点离地面的高度AB=（　　）
A、
asinαsinβ
sin(β-α)
B、
asinαsinβ
sin(α-β)
C、
asinαcosβ
sin(β-α)
D、
acosαsinβ
sin(α-β)
考点：解三角形
专题：计算题,解三角形
分析：先分别在直角三角形中表示出DB，BC，根据DC=DB-BC列等式求得AB．
解答： 解：依题意知，DB=
AB
tanα
，BC=
AB
tanβ
，
∴DC=DB-BC=AB（
1
tanα
-
1
tanβ
）=a，
∴AB=
asinαsinβ
sin(β-α)
，
故选：A．
点评：本题主要考查了解三角形的实际应用．把实际问题转化为三角形的问题，是常用思路．
练习册系列答案
相关题目
若直线y=（a2-a）x+a+1与直线y=2x+3平行，则a的值为（　　）
A、-1B、2C、-1或2D、-2
已知函数f（x）=cos x•sin（x+
π
3
）-
3
cos2x+
3
4
，x∈R．
（1）若0＜α＜
π
2
，且sinα=
3
2
，求f（α）的值；
（2）求函数f（x）的单调递增区间．
设x，y为正实数，若
4
y
+
1
x
=2，则2x+y的最小值是
 
．
函数f（x）=ax（a＞0，a≠1）在区间[1，2]上的最大值比最小值大
a
3
，
（1）求a的值；
（2）求f（2）的值．
已知角α的终边经过点（3，-4），则tan
α
2
=（　　）
A、-
1
3
B、-
1
2
C、2
D、3
在△ABC中，a、b、c分别是A、B、C三内角所对应的边，若a2+c2-b2+ac=0，则∠B=
 
．
已知集合A={2，3，4，5}，B={3，5，6}，则A∩B=（　　）
A、{3}
B、{2，4}
C、{2，3，4，5，6}
D、{3，5}
设集合U={1，2，3，4，5}，A={1，2，3}，B={2，5}，则（∁UA）∩（∁UB）=（　　）
A、{2}B、{2，3}
C、{4}D、{1，3}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网