题目内容
设x,y为正实数,若
+
=2,则2x+y的最小值是 .
| 4 |
| y |
| 1 |
| x |
考点:基本不等式在最值问题中的应用,基本不等式
专题:不等式的解法及应用
分析:根据
+
=2可得2x+y=(2x+y)(
+
),然后展开,利用基本不等式可求出最值,注意等号成立的条件.
| 4 |
| y |
| 1 |
| x |
| 4 |
| y |
| 1 |
| x |
解答:
解:∵两个正实数x,y满足
+
=2可得2x+y=
(2x+y)(
+
)=
(2+4+
+
)≥3+
=3+2
,当且仅当
=
,
+
=2时取等号,
故2x+y的最小值是3+2
.
故答案为:3+2
.
| 4 |
| y |
| 1 |
| x |
| 1 |
| 2 |
| 4 |
| y |
| 1 |
| x |
| 1 |
| 2 |
| 8x |
| y |
| y |
| x |
|
| 2 |
| 8x |
| y |
| y |
| x |
| 4 |
| y |
| 1 |
| x |
故2x+y的最小值是3+2
| 2 |
故答案为:3+2
| 2 |
点评:本题主要考查了基本不等式的应用,解题的关键是“1”的活用,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
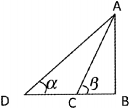 如图D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点的仰角分别为β,α(α<β),则A点离地面的高度AB=( )
如图D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点的仰角分别为β,α(α<β),则A点离地面的高度AB=( )A、
| ||
B、
| ||
C、
| ||
D、
|
以下说法正确的是( )
| A、正数的n次方根是正数 |
| B、负数的n次方根是负数 |
| C、0的n次方根是0(其中n>1且n∈N*) |
| D、负数没有n次方根 |