题目内容
函数f(x)=ax(a>0,a≠1)在区间[1,2]上的最大值比最小值大
,
(1)求a的值;
(2)求f(2)的值.
| a |
| 3 |
(1)求a的值;
(2)求f(2)的值.
考点:指数函数单调性的应用
专题:函数的性质及应用
分析:当a>1时,由题意可得a2-a=
,由此解得a的值.当0<a<1时,由题意可得a-a2=
,由此解得a的值,综合可得结论.
| a |
| 3 |
| a |
| 3 |
解答:
解:当a>1时,函数y=ax(a>0,a≠1)在[1,2]上是增函数,
由题意可得a2-a=
,
解得a=
.
当0<a<1时,函数y=ax(a>0,a≠1)在[1,2]上是减函数,
由题意可得a-a2=
,
解得a=
.
综上可得,a=
,或 a=
.
(2)由(1)得a=
时,f(2)=
,
a=
时,f(2)=
.
由题意可得a2-a=
| a |
| 3 |
解得a=
| 4 |
| 3 |
当0<a<1时,函数y=ax(a>0,a≠1)在[1,2]上是减函数,
由题意可得a-a2=
| a |
| 3 |
解得a=
| 2 |
| 3 |
综上可得,a=
| 4 |
| 3 |
| 2 |
| 3 |
(2)由(1)得a=
| 2 |
| 3 |
| 4 |
| 9 |
a=
| 4 |
| 3 |
| 16 |
| 9 |
点评:本题主要考查指数函数的单调性和特殊点,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
函数f(x)是定义域在R上的奇函数.若x≥0时f(x)=x2+2x,则f(-2)等于( )
| A、8 | B、4 | C、-8 | D、0 |
化简3
的结果为( )
| (-5)2 |
| A、15 | ||
B、3
| ||
C、-3
| ||
| D、-15 |
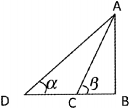 如图D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点的仰角分别为β,α(α<β),则A点离地面的高度AB=( )
如图D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点的仰角分别为β,α(α<β),则A点离地面的高度AB=( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合{x|x2+ax+b=0}={1},则函数y=x
的值域为( )
| a |
| b |
| A、(0,+∞) |
| B、(-∞,0)∪(0,+∞) |
| C、(-∞,0) |
| D、R |
命题p:?x∈R,log2x>0,命题q:?x0∈R,2x0<0,则下列命题为真命题的是( )
| A、p∨q | B、p∧q |
| C、(¬p)∧q | D、p∨(¬q) |