题目内容
已知函数f(x)=cos x•sin(x+
)-
cos2x+
,x∈R.
(1)若0<α<
,且sinα=
,求f(α)的值;
(2)求函数f(x)的单调递增区间.
| π |
| 3 |
| 3 |
| ||
| 4 |
(1)若0<α<
| π |
| 2 |
| ||
| 2 |
(2)求函数f(x)的单调递增区间.
考点:三角函数中的恒等变换应用,复合三角函数的单调性
专题:三角函数的图像与性质
分析:(1)函数可化简为f(x)=
sin(2x-
),若0<α<
,且sinα=
,则f(α)=
.
(2)由2kπ-
≤2x-
≤2kπ+
即可推得增区间.
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
| ||
| 2 |
| ||
| 4 |
(2)由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解答:
解:(1)由已知,有
f(x)=cos x•(
sinx+
cosx)-
cos2x+
=
sin x•cos x-
cos2x+
=
sin 2x-
(1+cos 2x)+
=
sin 2x-
cos 2x
=
sin(2x-
),
(1)若0<α<
,且sinα=
,则f(α)=
(2)由2kπ-
≤2x-
≤2kπ+
可得增区间为:[kπ-
,kπ+
],k∈Z
f(x)=cos x•(
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 4 |
=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
=
| 1 |
| 4 |
| ||
| 4 |
| ||
| 4 |
=
| 1 |
| 4 |
| ||
| 4 |
=
| 1 |
| 2 |
| π |
| 3 |
(1)若0<α<
| π |
| 2 |
| ||
| 2 |
| ||
| 4 |
(2)由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
点评:本题主要考察了三角函数中的恒等变换应用,复合三角函数的单调性,属于基础题.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
下列函数中,既是偶函数又在(-∞,0)上单调递增的是( )
| A、y=x3 | ||
| B、y=cosx | ||
C、y=(
| ||
| D、y=x2 |
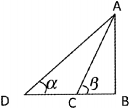 如图D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点的仰角分别为β,α(α<β),则A点离地面的高度AB=( )
如图D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点的仰角分别为β,α(α<β),则A点离地面的高度AB=( )A、
| ||
B、
| ||
C、
| ||
D、
|