题目内容
在△ABC中，a、b、c分别是A、B、C三内角所对应的边，若a2+c2-b2+ac=0，则∠B= ．
考点：余弦定理
专题：解三角形
分析：利用余弦定理表示出cosB，把已知等式代入计算求出cosB的值，即可确定出B的度数．
解答：
解：∵△ABC中，a2+c2-b2+ac=0，即a2+c2-b2=-ac，
∴cosB=
=-
，
则∠B=120°，
故答案为：120°
∴cosB=
| a2+c2-b2 |
| 2ac |
| 1 |
| 2 |
则∠B=120°，
故答案为：120°
点评：此题考查了余弦定理，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
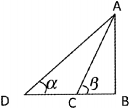如图D，C，B三点在地面同一直线上，DC=a，从C，D两点测得A点的仰角分别为β，α（α＜β），则A点离地面的高度AB=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
以下说法正确的是（ ）
| A、正数的n次方根是正数 |
| B、负数的n次方根是负数 |
| C、0的n次方根是0（其中n＞1且n∈N*） |
| D、负数没有n次方根 |
已知集合{x|x2+ax+b=0}={1}，则函数y=x
的值域为（ ）
| a |
| b |
| A、（0，+∞） |
| B、（-∞，0）∪（0，+∞） |
| C、（-∞，0） |
| D、R |