题目内容
19．已知函数$f（x）=\frac{{3-{x^2}}}{e^x}$在区间（m，m+2）上单调递减，则实数m的取值范围为[-1，1]．分析 求出函数的导数，解关于导函数的不等式，求出函数的单调区间，从而得到（m，m+2）⊆（-2，3），求出m的范围即可．
解答 解：f′（x）=$\frac{（x-3）（x+1）}{{e}^{x}}$，
令f′（x）＜0，解得：-1＜x＜3，
故f（x）在（-1，3）递减，
故（m，m+2）⊆（-1，3），
故$\left\{\begin{array}{l}{m≥-1}\\{m+2≤3}\end{array}\right.$，解得：-1≤m≤1，
故答案为：[-1，1]．
点评 本题考查了函数的单调性问题，考查导数的应用以及集合的包含关系，是一道基础题．
练习册系列答案
相关题目
10．已知数列{an}的前n项和Sn=2n-1，则数列{log2an}的前10项和等于（ ）
| A． | 1023 | B． | 55 | C． | 45 | D． | 35 |
7．对于常数m、n，“mn＜0”是“方程mx2+ny2=10的曲线是双曲线”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
14．过抛物线y2=4x的焦点的直线与圆x2+y2-4x-2y=0相交，截得弦长最长时的直线方程为（ ）
| A． | x-y-1=0 | B． | x+y-1=0 | C． | x-y+1=0 | D． | x+y+1=0 |
11．已知$f（x）=sin（ωx+ϕ）（ω＞0，|ϕ|＜\frac{π}{2}）$的最小正周期为π，若其图象向左平移$\frac{π}{3}$个单位后关于y轴对称，则（ ）
| A． | $ω=2，ϕ=\frac{π}{3}$ | B． | $ω=2，ϕ=\frac{π}{6}$ | C． | $ω=4，ϕ=\frac{π}{6}$ | D． | $ω=2，ϕ=-\frac{π}{6}$ |
8．
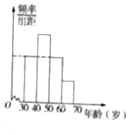韩国民意调查机构“盖洛普韩国”2016年11月公布的民调结果显示，受“闺蜜门”时间影响，韩国总统朴槿惠的民意支持率持续下跌，在所调查的1000个对象中，年龄在[20，30）的群体有200人，支持率为0%，年龄在[30，40）和[40，50）的群体中，支持率均为3%；年龄在[50，60）和[60，70）的群体中，支持率分别为6%和13%，若在调查的对象中，除[20，30）的群体外，其余各年龄层的人数分布情况如频率分布直方图所示，其中最后三组的频数构成公差为100的等差数列．
（1）依频率分布直方图求出图中各年龄层的人数
（2）请依上述支持率完成下表：
根据表中的数据，能否在犯错误的概率不超过0.001的前提下认为年龄与支持率有关？
附表：
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d 参考数据：125×33=15×275，125×97=25×485）
韩国民意调查机构“盖洛普韩国”2016年11月公布的民调结果显示，受“闺蜜门”时间影响，韩国总统朴槿惠的民意支持率持续下跌，在所调查的1000个对象中，年龄在[20，30）的群体有200人，支持率为0%，年龄在[30，40）和[40，50）的群体中，支持率均为3%；年龄在[50，60）和[60，70）的群体中，支持率分别为6%和13%，若在调查的对象中，除[20，30）的群体外，其余各年龄层的人数分布情况如频率分布直方图所示，其中最后三组的频数构成公差为100的等差数列．（1）依频率分布直方图求出图中各年龄层的人数
（2）请依上述支持率完成下表：
| 年龄分布 是否支持 | [30，40）和[40，50） | [50，60）和[60，70） | 合计 |
| 支持 | 15 | 25 | 40 |
| 不支持 | 485 | 275 | 760 |
| 合计 | 500 | 300 | 800 |
附表：
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
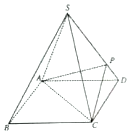如图所示，四棱锥S-ABCD的底面是正方形，每条侧棱的长都是底面边长的$\sqrt{2}$倍，点P在侧棱SD上，且SP=3PD．