Question

4．已知AD为△ABC边BC的中线，且$\overrightarrow{AB}•\overrightarrow{AC}=-16，|{\overrightarrow{BC}}|=10$，则$|{\overrightarrow{AD}}|$=（　　）

• A． 2
• B． 3
• C． 4
• D． 6

Answer 1

分析 可画出图形，对$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$的两边平方即可求出${\overrightarrow{AC}}^{2}+{\overrightarrow{AB}}^{2}=68$，而对$\overrightarrow{AD}=\frac{1}{2}（\overrightarrow{AB}+\overrightarrow{AC}）$的两边平方，即可求出${\overrightarrow{AD}}^{2}$的值，从而求出$|\overrightarrow{AD}|$的值．

解答 解：如图，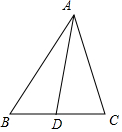
$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$；
∴${\overrightarrow{BC}}^{2}={\overrightarrow{AC}}^{2}-2\overrightarrow{AB}•\overrightarrow{AC}+{\overrightarrow{AB}}^{2}$；
∴$100={\overrightarrow{AC}}^{2}+32+{\overrightarrow{AB}}^{2}$；
∴${\overrightarrow{AC}}^{2}+{\overrightarrow{AB}}^{2}=68$；
又$\overrightarrow{AD}=\frac{1}{2}（\overrightarrow{AB}+\overrightarrow{AC}）$；
∴${\overrightarrow{AD}}^{2}=\frac{1}{4}（{\overrightarrow{AB}}^{2}+2\overrightarrow{AB}•\overrightarrow{AC}+{\overrightarrow{AC}}^{2}）$=$\frac{1}{4}×（68-32）=9$；
∴$|\overrightarrow{AD}|=3$．
故选B．

点评 考查向量减法的几何意义，向量加法的平行四边形法则，以及向量数量积的运算．