题目内容
9.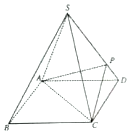 如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,点P在侧棱SD上,且SP=3PD.
如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,点P在侧棱SD上,且SP=3PD.(1)求证:AC⊥SD;
(2)若$AB=\sqrt{2}$,求三棱锥D-ACP的体积;
(3)侧棱SC上是否存在一点E,使得BE∥平面PAC,若存在,求$\frac{SE}{EC}$的值;若不存在,试说明理由.
分析 (1)法一(几何法):连BD,设AC交BD于O,则SO⊥AC,在正方形ABCD中,AC⊥BD,根据线面垂直的判定定理可知AC⊥平面SBD,SD?平面SBD,根据线面垂直的性质可知AC⊥SD.
法二(向量法):以O为原点,以$\overrightarrow{OB}$、$\overrightarrow{OC}$、$\overrightarrow{OS}$分别为x轴、y轴、z轴的正方向,建立空间直角坐标系,利用向量法能证明AC⊥SD.
(2)三棱锥D-ACP的体积VD-ACP=VP-ADC,由此能求出结果.
(3)求出平面PAC的一个法向量,利用向量法能求出当$\frac{SE}{EC}$=2时,BE∥平面PAC.
解答 证明:(1)证法一:(几何法)连结BD,设AC交BD于O,连结SO,
∵四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,
∴SO⊥AC,SO⊥BD,
∵AC∩BD=O,∴SO⊥底面ABCD,
∵AC?底面ABCD,∴SO⊥AC.
在正方形ABCD中,AC⊥BD,
∵SO∩BD=O,∴AC⊥平面SBD,
∵SD?平面SBD,∴AC⊥SD.
证法二:(向量法)以O为原点,以$\overrightarrow{OB}$、$\overrightarrow{OC}$、$\overrightarrow{OS}$分别为x轴、y轴、z轴的正方向,建立空间直角坐标系,
设设底面边长为a,则高SO=$\frac{\sqrt{6}}{2}$a.则S(0,0,$\frac{\sqrt{6}}{2}$a),D(-$\frac{\sqrt{2}}{2}$a,0,0),C(0,$\frac{\sqrt{2}}{2}$a,0),
$\overrightarrow{SD}$=(-$\frac{\sqrt{2}}{2}a$,0,-$\frac{\sqrt{6}}{2}a$),$\overrightarrow{AC}$=(0,$\frac{\sqrt{2}}{2}a$,0),
$\overrightarrow{AC}•\overrightarrow{SD}$=0,
∴AC⊥SD.
解:(2)∵$AB=\sqrt{2}$,∴SA=SB=SC=SD=2,
∵点P在侧棱SD上,且SP=3PD,∴P到平面ADC的距离h=$\frac{1}{4}PO=\frac{1}{4}\sqrt{4-1}=\frac{\sqrt{3}}{4}$,
∴三棱锥D-ACP的体积:
VD-ACP=VP-ADC=$\frac{1}{3}×h×{S}_{△ADC}$=$\frac{1}{3}×\frac{\sqrt{3}}{4}×\frac{1}{2}×\sqrt{2}×\sqrt{2}$=$\frac{\sqrt{3}}{12}$.
(3)P(-$\frac{3\sqrt{2}}{8}$a,$\frac{\sqrt{6}}{8}$a),$\overrightarrow{OC}$=(0,$\frac{\sqrt{2}}{2}a$,0),$\overrightarrow{SD}$=(-$\frac{\sqrt{2}}{2}a$,0,-$\frac{\sqrt{6}}{2}a$),$\overrightarrow{AC}$=(0,$\frac{\sqrt{2}}{2}a$,0),$\overrightarrow{AP}$=(-$\frac{3\sqrt{2}}{8}$a,0,$\frac{\sqrt{6}}{8}a$),
$\overrightarrow{AC}•\overrightarrow{SD}$=0,$\overrightarrow{SD}•$$\overrightarrow{AP}$=0,
∴AC⊥SD,AP⊥SD,
∴平面PAC的一个法向量为$\overrightarrow{DS}$=($\frac{\sqrt{2}}{2}a$,0,$\frac{\sqrt{6}}{2}a$),
在棱SC上存在一点E使BE∥平面PAC.,
∵$\overrightarrow{DS}$=($\frac{\sqrt{2}}{2}a$,0,$\frac{\sqrt{6}}{2}a$)是平面PAC的一个法向量,且$\overrightarrow{CS}$=(0,-$\frac{\sqrt{2}}{2}$a,$\frac{\sqrt{6}}{2}a$),
设$\overrightarrow{CE}$=t$\overrightarrow{CS}$(0≤t≤1),
$\overrightarrow{BE}=\overrightarrow{BC}+\overrightarrow{CE}=\overrightarrow{BC}+t\overrightarrow{CS}$=(-$\frac{\sqrt{2}}{2}a,\frac{\sqrt{2}}{2}a(1-t),\frac{\sqrt{6}}{2}at$),
由$\overrightarrow{BE}•\overrightarrow{DS}$=-$\frac{1}{2}a+\frac{3}{2}at$=0,解得t=$\frac{1}{3}$,
∴当$\frac{SE}{EC}$=2时,BE∥平面PAC.
点评 本题考查线线垂直的证明,考查三棱锥的体积的求法,考查满足线面平行的点的位置的确定,考查空间想象能力、运算求解能力、推理论证能力,考查数形结合思想、化归与转化思想,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 3 | B. | 5 | C. | 7 | D. | 8 |
| A. | |b|=$\sqrt{2}$ | B. | -1<b≤1或b=-$\sqrt{2}$ | C. | -1≤b≤$\sqrt{2}$ | D. | 0<b≤1或b=$\sqrt{2}$ |
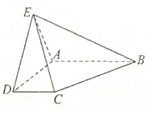 如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.
如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.