题目内容
14.过抛物线y2=4x的焦点的直线与圆x2+y2-4x-2y=0相交,截得弦长最长时的直线方程为( )| A. | x-y-1=0 | B. | x+y-1=0 | C. | x-y+1=0 | D. | x+y+1=0 |
分析 求出抛物线的焦点和圆心坐标,利用直线过圆心时,弦最长为圆的直径,用两点式求直线方程.
解答 解:抛物线y2=4x的焦点为(1,0),圆x2+y2-4x+2y=0 即 (x-2)2+(y+1)2=5,圆心为(2,-1),
由弦长公式可知,要使截得弦最长,需圆心到直线的距离最小,故直线过圆心时,弦最长为圆的直径.
由两点式得所求直线的方程 $\frac{y-0}{-1-0}$=$\frac{x-1}{2-1}$,即 x+y-1=0,
故选:B.
点评 本题考查用两点式求直线方程的方法,判断直线过圆心时,弦最长是解题的关键.

练习册系列答案
相关题目
4.要得到函数$f(x)=sin2x+\sqrt{3}cos2x({x∈R})$的图象,可将y=2sin2x的图象向左平移( )
| A. | $\frac{π}{6}$个单位 | B. | $\frac{π}{3}$个单位 | C. | $\frac{π}{4}$个单位 | D. | $\frac{π}{12}$个单位 |
5.已知直线x+ylog4a=0与直线2x-y-3=0平行,则a的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | 4 | D. | 16 |
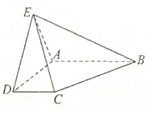 如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.
如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.