题目内容
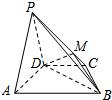 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4| 5 |
(1)求VP-ABCD;
(2)求PB与平面ABCD所成的角;
(3)求证:平面MBD⊥平面PAD.
考点:直线与平面所成的角,棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)首先对面面垂直转化出线面垂直进一步求出锥体的高,及锥体的底面积,进一步求出锥体的体积.
(2)利用(1)的线面垂直,首先确定线面的夹角进一步利用所给的条件求出夹角的大小.
(3)直接根据线面垂直的判定,进一步转化出面面垂直.
(2)利用(1)的线面垂直,首先确定线面的夹角进一步利用所给的条件求出夹角的大小.
(3)直接根据线面垂直的判定,进一步转化出面面垂直.
解答:
解:(1)在四棱锥P-ABCD中,平面PAD⊥平面ABCD,
连接BD,过P点做PE⊥AD,
所以:PE⊥平面ABCD.
△PAD是等边三角形,已知BD=2AD=8,
所以:AD=4,
进一步求得:PE=2
,
在四边形ABCD中,AB∥CD,AB=2DC=4
,AD=4
所以:AD2+BD2=AB2
则:△ABD是直角三角形.
设△ABD的高为h,利用面积相等,
AD•BD=AB•h
解得:h=
所以:VP-ABCD=
S梯形ABCD•PE
=16
(2)由(1)得:PE⊥平面ABCD
所以:PB与平面ABCD所成的角
即∠PBE就是所求.
在△BDE中,连接BE,BE=
解得:BE=2
所以:tan∠PBE=
=
所以PB与平面ABCD所成的角为:arctan
证明:(3)已求得AD2+BD2=AB2
所以:AD⊥BD
PE⊥平面ABCD
BD?平面ABCD
所以:PE⊥BD
则:BD⊥平面PAD.
由于BD?平面MBD
所以:平面MBD⊥平面PAD
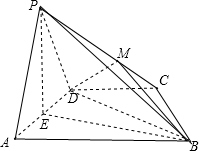
连接BD,过P点做PE⊥AD,
所以:PE⊥平面ABCD.
△PAD是等边三角形,已知BD=2AD=8,
所以:AD=4,
进一步求得:PE=2
| 3 |
在四边形ABCD中,AB∥CD,AB=2DC=4
| 5 |
所以:AD2+BD2=AB2
则:△ABD是直角三角形.
设△ABD的高为h,利用面积相等,
AD•BD=AB•h
解得:h=
8
| ||
| 5 |
所以:VP-ABCD=
| 1 |
| 3 |
=16
| 3 |
(2)由(1)得:PE⊥平面ABCD
所以:PB与平面ABCD所成的角
即∠PBE就是所求.
在△BDE中,连接BE,BE=
| AD2+BD2 |
解得:BE=2
| 17 |
所以:tan∠PBE=
| PE |
| BE |
| ||
| 17 |
所以PB与平面ABCD所成的角为:arctan
| ||
| 17 |
证明:(3)已求得AD2+BD2=AB2
所以:AD⊥BD
PE⊥平面ABCD
BD?平面ABCD
所以:PE⊥BD
则:BD⊥平面PAD.
由于BD?平面MBD
所以:平面MBD⊥平面PAD

点评:本题考查的知识要点:线面垂直与面面垂直之间的转化,棱锥的体积的运算,线面夹角的应用,勾股定理逆定理及相关的运算问题.属于基础题型.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
函数f(x)=x2+4x+5的单调递增区间是( )
| A、(-∞,-2] |
| B、[-2,+∞) |
| C、[-5,-2] |
| D、[-2,1] |
已知四棱锥S-ABCD的所有棱长都相等,E是SB的中点,则AE,SD所成的角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
方程x+y+z=10的正整数解的个数( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在体积为
如图,在体积为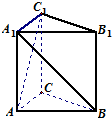 直三棱柱ABC-A1B1C1中,AC=AB=AA1,且异面直线AC1与A1B所成的角为60°,则∠CAB等于
直三棱柱ABC-A1B1C1中,AC=AB=AA1,且异面直线AC1与A1B所成的角为60°,则∠CAB等于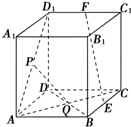 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、P、Q分别是BC、C1D1、AD1、BD的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、P、Q分别是BC、C1D1、AD1、BD的中点.