题目内容

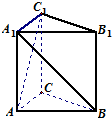直三棱柱ABC-A1B1C1中，AC=AB=AA1，且异面直线AC1与A1B所成的角为60°，则∠CAB等于
 
．
考点：异面直线及其所成的角
专题：空间角
分析：由已知条件，构造正方体ABDC-A1B1D1C1，由此能求出∠CAB=90°．
解答： 解：由已知条件，构造正方体ABDC-A1B1D1C1，
满足条件AC=AB=AA1，
且异面直线AC1与A1B所成的角为60°，
∴∠CAB=90°．
故答案为：90°．
点评：本题考查异面直线所成角的大小的求法，是基础题，解题时要认真审题，注意构造法的合理运用．
练习册系列答案
相关题目
设函数f（x）=|x2-2x-3|，x∈R．
（1）在区间[-2，4]上画出函数f（x）的图象；
（2）写出该函数在R上的单调区间．
已知在△ABC中，求证：
a2-b2
c2
=
sin(A-B)
sinC
．
若集合A={x||x-a|≤1}与B={x||2x-5|≥3}，且A∩B=O，求实数a的取值范围．
已知函数f（x）=x2+a|x-b|-1（x∈R）．
（1）若函数f（x）为偶函数，求实数b的值；
（2）在（1）的条件下，若函数f（x）在（0，+∞）不单调，求实数a的取值范围；
（3）当a=1时，先求函数f（x）的最小值g（b），再判断并证明函数g（b）的奇偶性．
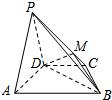在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB∥CD，△PAD是等边三角形，已知BD=2AD=8，AB=2DC=4
5
，设M是PC上的一点．
（1）求VP-ABCD；
（2）求PB与平面ABCD所成的角；
（3）求证：平面MBD⊥平面PAD．
平行六面体ABCD-A1B1C1D1中，以顶点A为端点的三条棱长度都为2，且两两夹角为60°，则DB1和C1A1所成角大小为
 
．
在曲线y=x3-x上有两个点O（0，0），A（2，6），若I是
OA
上的一点，并使得△AOI的面积最大，求I点的坐标．
在长方体ABCD-A1B1C1D1中，其中ABCD是正方形，AA1＞AB．设点A到直线B1D的距离和到平面DCB1A1的距离分别为d1，d2，则
d1
d2
的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网