题目内容
函数f(x)=3x+log
(-x)的零点所在区间为 .
| 1 |
| 2 |
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:易知函数f(x)=3x+log
(-x)在定义域(-∞,0)上是增函数且连续,再由函数零点的判定定理求出区间即可.
| 1 |
| 2 |
解答:
解:易知函数f(x)=3x+log
(-x)在定义域(-∞,0)上是增函数,
且函数f(x)=3x+log
(-x)在定义域(-∞,0)上连续;
而f(-1)=
+0=
>0,
f(-2)=
-1=-
<0;
故f(-1)f(-2)<0;
故函数f(x)=3x+log
(-x)的零点所在区间为(-2,-1);
故答案为:(-2,-1).
| 1 |
| 2 |
且函数f(x)=3x+log
| 1 |
| 2 |
而f(-1)=
| 1 |
| 3 |
| 1 |
| 3 |
f(-2)=
| 1 |
| 9 |
| 8 |
| 9 |
故f(-1)f(-2)<0;
故函数f(x)=3x+log
| 1 |
| 2 |
故答案为:(-2,-1).
点评:本题考查了函数零点的判定定理的应用,属于基础题.

练习册系列答案
相关题目
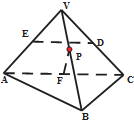 如图所示,正三棱锥V-ABC中,D,E,F分别是VC,VA,AC的中点,P为VB上任意一点,则直线DE与PF所成的角的大小是( )
如图所示,正三棱锥V-ABC中,D,E,F分别是VC,VA,AC的中点,P为VB上任意一点,则直线DE与PF所成的角的大小是( )| A、30° | B、60° |
| C、90° | D、随P点的变化而变化 |
若存在x∈[-2,3],使不等式4x-x2≥a成立,则实数a的取值范围是( )
| A、[-8,+∞) |
| B、[3,+∞) |
| C、(-∞,-12] |
| D、(-∞,4] |
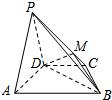 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4