题目内容
方程x+y+z=10的正整数解的个数( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:计数原理的应用,组合及组合数公式
专题:排列组合
分析:本题转化为把10个球放在三个不同的盒子里,有多少种方法,利用隔板法即可求出.
解答:
解:问题中的x、y、z看作是三个盒子,问题则转化为把10个球放在三个不同的盒子里,有多少种方法.
将10个球排一排后,中间插入两块隔板将它们分成三堆球,使每一堆至少一个球.
隔板不能相邻,也不能放在两端,只能放在中间的9个空内.
因此共有C92=36种.
故选:A
将10个球排一排后,中间插入两块隔板将它们分成三堆球,使每一堆至少一个球.
隔板不能相邻,也不能放在两端,只能放在中间的9个空内.
因此共有C92=36种.
故选:A
点评:本题考查了排列组合问题,本题转化为类把10个球放在三个不同的盒子里,有多少种方法是关键,属于中档题.

练习册系列答案
相关题目
若存在x∈[-2,3],使不等式4x-x2≥a成立,则实数a的取值范围是( )
| A、[-8,+∞) |
| B、[3,+∞) |
| C、(-∞,-12] |
| D、(-∞,4] |
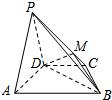 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4