题目内容
已知:3sinβ=sin(2α+β),求tan(α+β)cotα的值.
考点:同角三角函数基本关系的运用,两角和与差的正弦函数
专题:三角函数的求值
分析:已知等式两边中的角度变形后,利用两角和与差的正弦函数公式化简,整理后利用同角三角函数间的基本关系变形即可求出所求式子的值.
解答:
解:已知等式3sinβ=sin(2α+β),
变形得:3sin[(α+β)-α]=sin[(α+β)+α],
化简得:3sin(α+β)cosα-3cos(α+β)sinα=sin(α+β)cosα+cos(α+β)sinα,
即2sin(α+β)cosα=4cos(α+β)sinα
两边同时除以2cosαcos(α+β)得:tan(α+β)=2tanα,
则tan(α+β)cotα=
=2.
变形得:3sin[(α+β)-α]=sin[(α+β)+α],
化简得:3sin(α+β)cosα-3cos(α+β)sinα=sin(α+β)cosα+cos(α+β)sinα,
即2sin(α+β)cosα=4cos(α+β)sinα
两边同时除以2cosαcos(α+β)得:tan(α+β)=2tanα,
则tan(α+β)cotα=
| tan(α+β) |
| tanα |
点评:此题考查了同角三角函数基本关系的运用,以及两角和与差的正弦函数公式,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
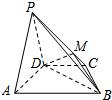 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4