题目内容
已知四棱锥S-ABCD的所有棱长都相等,E是SB的中点,则AE,SD所成的角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:作SO⊥平面ABCD,交平面ABCD于点O,以O为原点,OS为z轴,建立如图所示的空间直角坐标系,利用向量法能求出AE,SD所成的角的正弦值.
解答:
解: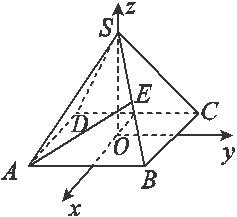 作SO⊥平面ABCD,交平面ABCD于点O,
作SO⊥平面ABCD,交平面ABCD于点O,
以O为原点,OS为z轴,建立如图所示的空间直角坐标系,
令四棱锥的棱长为2,
则A(1,-1,0),D(-1,-1,0),S(0,0,
),
E(
,
,
),
∴
=(-
,
,
),
=(-1,-1,-
),
∴设AE,SD所成的角为θ,
cosθ=|cos<
,
>|=
=
,
sinθ=
=
.
∴AE,SD所成的角的正弦值为
.
故选:B.
 作SO⊥平面ABCD,交平面ABCD于点O,
作SO⊥平面ABCD,交平面ABCD于点O,以O为原点,OS为z轴,建立如图所示的空间直角坐标系,
令四棱锥的棱长为2,
则A(1,-1,0),D(-1,-1,0),S(0,0,
| 2 |
E(
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴
| AE |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| SD |
| 2 |
∴设AE,SD所成的角为θ,
cosθ=|cos<
| AE |
| SD |
|
| ||||
|
|
| ||
| 3 |
sinθ=
1-(
|
| ||
| 3 |
∴AE,SD所成的角的正弦值为
| ||
| 3 |
故选:B.
点评:本题考查异面直线所成角的求法,是基础题,解题时要注意线线、线面、面面间的位置关系和性质的合理运用,注意空间思维能力的培养.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
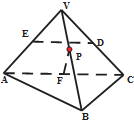 如图所示,正三棱锥V-ABC中,D,E,F分别是VC,VA,AC的中点,P为VB上任意一点,则直线DE与PF所成的角的大小是( )
如图所示,正三棱锥V-ABC中,D,E,F分别是VC,VA,AC的中点,P为VB上任意一点,则直线DE与PF所成的角的大小是( )| A、30° | B、60° |
| C、90° | D、随P点的变化而变化 |
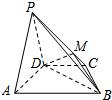 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4