题目内容
设各项均为正数的无穷数列{an},{bn}满足:对任意n∈N*都有2bn=an+an+1且an+12=bn•bn+1,
(1)求证:数列{
}是等差数列;
(2)设a1=1,a2=3,b1=2,求{an}和{bn}的通项公式.
(1)求证:数列{
| bn |
(2)设a1=1,a2=3,b1=2,求{an}和{bn}的通项公式.
考点:等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件得到bnbn-1+bnbn+1+2
=4bn•bn,由此能证明数列{
}是等差数列.
(2)由已知条件推导出
=
(n+1),由此能求出{an}和{bn}的通项公式.
| bn-1•bn•bn•bn+1 |
| bn |
(2)由已知条件推导出
| bn |
| ||
| 2 |
解答:
(1)证明:an+an+1=2bn,①
bnbn+1=an+12,②
②式两边开方得:an+1=
=
•
,③
①式两边平方,展开,然后将③代入,得:
bnbn-1+bnbn+1+2
=4bn•bn,④
整理,得
+
=2
,
∴数列{
}是等差数列.
(2)∵a1=1,a2=3,b1=2,且an+12=bn•bn+1,
∴b2=
=
,
-
=
-
=
,
∴
=
+(n-1)×
=
(n+1),
∴bn=
(n+1)2,
∵an+12=bn•bn+1,
∴an=
=
=
n(n+1).
bnbn+1=an+12,②
②式两边开方得:an+1=
| bnbn+1 |
| bn |
| bn+1 |
①式两边平方,展开,然后将③代入,得:
bnbn-1+bnbn+1+2
| bn-1•bn•bn•bn+1 |
整理,得
| bn-1 |
| bn+1 |
| bn |
∴数列{
| bn |
(2)∵a1=1,a2=3,b1=2,且an+12=bn•bn+1,
∴b2=
| a22 |
| b1 |
| 9 |
| 2 |
| b2 |
| b1 |
|
| 2 |
| ||
| 2 |
∴
| bn |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴bn=
| 1 |
| 2 |
∵an+12=bn•bn+1,
∴an=
| bn-1•bn |
|
| 1 |
| 2 |
点评:本题考查等差数列的证明,考查数列的通项公式的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
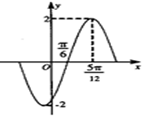 已知函数f(x)=Msin(ωx+φ)(x∈R,M>0,ω>0,|φ|<
已知函数f(x)=Msin(ωx+φ)(x∈R,M>0,ω>0,|φ|<