题目内容
11.若(x-$\sqrt{6}$)n展开式的第三项系数等于18,则n等于( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 根据展开式中第三项系数等于,列出方程求得n的值.
解答 解:∵(x-$\sqrt{6}$)n展开式的通项公式为Tr+1=${C}_{n}^{r}$•xn-r•${(-\sqrt{6})}^{r}$,
令r=2,得T3=${C}_{n}^{2}$•xn-2•${(-\sqrt{6})}^{2}$=6${C}_{n}^{2}$xn-2,
又展开式的第3项系数为6${C}_{n}^{2}$=18,
即${C}_{n}^{2}$=3,
∴$\frac{1}{2}$n(n-1)=3,
即n2-n-6=0,
解得n=3或n=-2(不合题意,舍去),
∴n等于3.
故选:D.
点评 本题主要考查了二项式定理的应用问题,解题时应用二项展开式的通项公式求展开式中某项的系数,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.在平面区域{(x,y)|0≤x≤1,1≤y≤2}内随机投入一点P,则点P的坐标(x,y)满足y≤2x的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
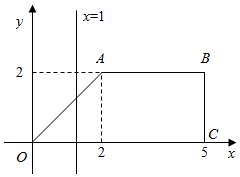 如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).
如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).