题目内容
1.在△ABC中,角A,B,C的对边分别是a,b,c,且 a=2,b=3,c=4,则$\frac{sin2C}{sinA}$=-1.分析 由正弦定理先求得sinC=2sinA,由余弦定理cosC=-$\frac{1}{4}$,代入所求即可求解.
解答 解:在△ABC中,由正弦定理可得:sinA:sinB:sinC=2:3:4
故有:sinC=2sinA
由余弦定理:cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{4+9-16}{12}$=-$\frac{1}{4}$,
∴$\frac{sin2C}{sinA}$=$\frac{2sinCcosC}{sinA}$=$\frac{2×2sinA×(-\frac{1}{4})}{sinA}$=-1.
故答案为:-1.
点评 此题考查了正弦定理,二倍角的正弦函数公式在解三角形中的应用,熟练掌握正弦定理是解本题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知集合A={x|x2-5x+6≤0},B={x∈Z|2x>1},则A∩B=( )
| A. | [2,3] | B. | (0,+∞) | C. | (0,2)∪(3,+∞) | D. | (0,2]∪[3,+∞) |
6.已知f(x)=lnx,则$f'(\frac{1}{e})$的值为( )
| A. | 1 | B. | -1 | C. | e | D. | $\frac{1}{e}$ |
10.已知两不共线的向量$\overrightarrow{a}$,$\overrightarrow{b}$,若对非零实数m,n有m$\overrightarrow{a}$+n$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$共线,则$\frac{m}{n}$=( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
11.若(x-$\sqrt{6}$)n展开式的第三项系数等于18,则n等于( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
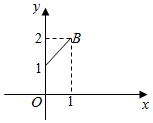 设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图所示的线段AB,则方程[f(x)]2=x的最大实数根的值为$\frac{11-\sqrt{21}}{2}$.
设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图所示的线段AB,则方程[f(x)]2=x的最大实数根的值为$\frac{11-\sqrt{21}}{2}$.