题目内容
6．在平面区域{（x，y）|0≤x≤1，1≤y≤2}内随机投入一点P，则点P的坐标（x，y）满足y≤2x的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
分析 作出不等式组对应的区域，利用几何概型的概率公式，即可得到结论．
解答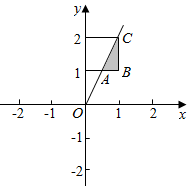 
解：不等式组$\left\{\begin{array}{l}{0≤x≤1}\\{1≤y≤2}\end{array}\right.$表示的平面区域为D的面积为1，
不等式y≤2x对应的区域为三角形ABC，
则三角形ABC的面积S=$\frac{1}{2}×\frac{1}{2}×1$=$\frac{1}{4}$，
则在区域D内任取一点P（x，y），则点P满足y≤2x的概率为$\frac{1}{4}$，
故选：A．
点评 本题主要考查二元一次不等式表示平面区域以及几何概型的概率计算，利用条件求出对应区域的面积是解决本题的关键．
练习册系列答案
相关题目
14．下列各组函数中，f（x）与g（x）表示同一函数的是（ ）
| A． | f（x）=x-1与g（x）=$\sqrt{{x}^{2}-2x+1}$ | B． | f（x）=x与g（x）=$\frac{{x}^{2}}{x}$ | ||
| C． | f（x）=x与g（x）=$\root{3}{x^3}$ | D． | f（x）=$\frac{{x}^{2}-4}{x-2}$与g（x）=x+2 |
1．不等式x2+x＜$\frac{a}{b}$+$\frac{b}{a}$ 对任意a，b∈（0，+∞）恒成立，则实数x的取值范围是（ ）
| A． | （-2，0） | B． | （-∞，-2）∪（1，+∞） | C． | （-2，1） | D． | （-∞，-4）∪（2，+∞） |
11．若（x-$\sqrt{6}$）n展开式的第三项系数等于18，则n等于（ ）
| A． | 6 | B． | 5 | C． | 4 | D． | 3 |
18．化简$\sqrt{9{x^2}-6x+1}-{（{\sqrt{3x-5}}）^2}$，结果是（ ）
| A． | 6x-6 | B． | -6x+6 | C． | -4 | D． | 4 |
15．若已知sinθ-cosθ=$\frac{\sqrt{5}}{3}$，那么sin3θ-cos3θ的值为（ ）
| A． | $\frac{\sqrt{5}}{27}$ | B． | $\frac{11}{27}$ | C． | $\frac{11}{27}\sqrt{5}$ | D． | $\frac{25}{17}$ |
16．如果x，y为实数，且x2-x+（y-1）2=0，则x的取值范围为（ ）
| A． | 任意实数 | B． | 负实数 | C． | 0＜x≤$\frac{1}{2}$ | D． | 0≤x≤1 |