题目内容
16．
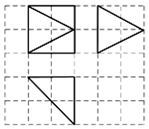如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，几何体的表面积为（ ）| A． | 4+2（$\sqrt{2}$+$\sqrt{3}$） | B． | 6+2（$\sqrt{2}$+$\sqrt{5}$） | C． | 10 | D． | 12 |
分析 首先还原几何体，然后计算表面积．
解答 解：由三视图得到几何体如图：
所以几何体的表面积为：$2×2+2×\frac{1}{2}×2×\sqrt{5}+\frac{1}{2}×2×2+\frac{1}{2}×2×2\sqrt{2}$=6+2（$\sqrt{2}+\sqrt{5}$）；
故选：B．
点评 本题考查了由几何体的三视图求几何体的表面积；关键是正确还原几何体，计算相关的数据求表面积．
练习册系列答案
相关题目
6．在（0，2π）内使sin x＞|cos x|的x的取值范围是（ ）
| A． | （$\frac{π}{4}$，$\frac{3π}{4}$） | B． | （$\frac{π}{4}$，$\frac{π}{2}$]∪（$\frac{5π}{4}$，$\frac{3π}{2}$] | C． | （$\frac{π}{4}$，$\frac{π}{2}$） | D． | （$\frac{5π}{4}$，$\frac{7π}{4}$） |
4．
如图是一个四面体的三视图，图中三个三角形均为直角三角形，且面积之和为8，则其外接球的表面积的最小值为（ ）
如图是一个四面体的三视图，图中三个三角形均为直角三角形，且面积之和为8，则其外接球的表面积的最小值为（ ）| A． | 16π | B． | 8π | C． | $\frac{32π}{3}$ | D． | $\frac{16π}{3}$ |
9．定积分$\int_0^4{\sqrt{16-{x^2}}}$dx表示（ ）
| A． | 半径为4的圆的面积 | B． | 半径为4的半圆的面积 | ||
| C． | 半径为4的圆面积的$\frac{1}{4}$ | D． | 半径为16的圆面积的$\frac{1}{4}$ |