题目内容
1.已知过抛物线C:x2=2py(p>0)的焦点F且斜率为$\frac{3}{4}$的直线与抛物线C在第一象限的交点为P,且|PF|=5.(1)求抛物线C的方程;
(2)过F且斜率不为0直线l交抛物线C于M,N两点,抛物线C的准线与x轴交于点K,求证:直线KM与KN关于y轴对称.
分析 (1)设P(x0,y0),过P作PA⊥y轴于A,分析可得${y_0}=\frac{p}{2}+3$,结合抛物的定义得$\frac{p}{2}+{y_0}=5$,解可得p的值,代入抛物线的方程即可得答案;
(2)根据题意,设直线KM和KN的斜率分别为k1,k2,由(1)得F与K的坐标,设直线l的方程为y=kx+1,将直线方程与抛物线方程联立可得x2-4kx-4=0,由根与系数的关系的关系分析可得,${k_1}+{k_2}=\frac{{{y_1}+1}}{x_1}+\frac{{{y_2}+1}}{x_2}=\frac{{2k{x_1}{x_2}+2({x_1}+{x_2})}}{{{x_1}{x_2}}}=\frac{-8k+8k}{{{x_1}{x_2}}}=0$,即可得证明.
解答 解:(1)设P(x0,y0),过P作PA⊥y轴于A,
∵直线PF的斜率为$\frac{3}{4}$,∴$cos∠AFP=\frac{3}{5}$,
∵|PF|=5,∴|PA|=3,则${y_0}=\frac{p}{2}+3$,
由抛物线的定义得$\frac{p}{2}+{y_0}=5$,得p=2
∴抛物线方程为x2=4y.
(2)证明:设直线KM和KN的斜率分别为k1,k2,
由(1)得F(0,1),K(0,-1),
设直线l的方程为y=kx+1,M(x1,y1),N(x2,y2),
∵k≠0,∴A与M不重合,
由$\left\{\begin{array}{l}{x^2}=4y\\ y=kx+1\end{array}\right.$,得x2-4kx-4=0,∴x1+x2=4k,x1x2=-4,
∵${k_1}+{k_2}=\frac{{{y_1}+1}}{x_1}+\frac{{{y_2}+1}}{x_2}=\frac{{2k{x_1}{x_2}+2({x_1}+{x_2})}}{{{x_1}{x_2}}}=\frac{-8k+8k}{{{x_1}{x_2}}}=0$,
∴直线KMG与KN关于y轴对称,
点评 本题考查直线与抛物线的位置关系,关键是求出抛物线的标准方程.

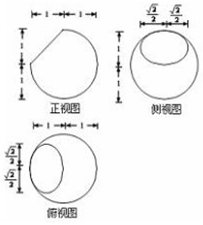 半径为1的球被一平面截去部分得一个几何体,其三视图和尺寸如图所示,则球心到该截面的距离为( )
半径为1的球被一平面截去部分得一个几何体,其三视图和尺寸如图所示,则球心到该截面的距离为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
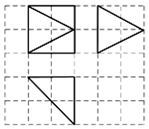 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,几何体的表面积为( )| A. | 4+2($\sqrt{2}$+$\sqrt{3}$) | B. | 6+2($\sqrt{2}$+$\sqrt{5}$) | C. | 10 | D. | 12 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,四边形ABCD中,∠CBD=α,∠C=β,∠A+β=π,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ
如图,四边形ABCD中,∠CBD=α,∠C=β,∠A+β=π,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ 设函数y=f(x)在区间[0,1]上的图象是连续不断的一条曲线,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算由曲线y=f(x)及直线x=0,x=1,y=0所围成部分的面积S,先生产两组(每组N个)区间[0,1]上均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得S的近似值为$\frac{{N}_{1}}{N}$.
设函数y=f(x)在区间[0,1]上的图象是连续不断的一条曲线,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算由曲线y=f(x)及直线x=0,x=1,y=0所围成部分的面积S,先生产两组(每组N个)区间[0,1]上均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得S的近似值为$\frac{{N}_{1}}{N}$.