题目内容
9．定积分$\int_0^4{\sqrt{16-{x^2}}}$dx表示（ ）| A． | 半径为4的圆的面积 | B． | 半径为4的半圆的面积 | ||
| C． | 半径为4的圆面积的$\frac{1}{4}$ | D． | 半径为16的圆面积的$\frac{1}{4}$ |
分析 设被积函数为y，得到x2+y2=16（0＜x＜4，y＞0），由此得到定积分值．
解答 解：设y=$\sqrt{16-{x}^{2}}$，整理得到x2+y2=16（0＜x＜4，y＞0），
所以定积分$\int_0^4{\sqrt{16-{x^2}}}$dx表示半径为4的圆面积的$\frac{1}{4}$；
故选C．
点评 本题考查了定积分的几何意义；属于基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
16．
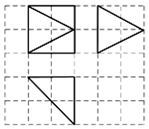如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，几何体的表面积为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，几何体的表面积为（ ）| A． | 4+2（$\sqrt{2}$+$\sqrt{3}$） | B． | 6+2（$\sqrt{2}$+$\sqrt{5}$） | C． | 10 | D． | 12 |
17．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\sqrt{5}$，圆心在x轴的正半轴上的圆M与双曲线的渐近线相切，且圆M的半径为2，则以圆M的圆心为焦点的抛物线的标准方程为（ ）
| A． | y2=8$\sqrt{5}$x | B． | y2=4$\sqrt{5}$x | C． | y2=2$\sqrt{5}$x | D． | y2=$\sqrt{5}$x |
PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．我国PM2.5标准采用世卫组织设定的最宽限值，即PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米～75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．