题目内容
已知A(1,0,0),B(0,-1,1),
+λ
与
的夹角为60°,则λ的值为( )
| OA |
| OB |
| OB |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、±
|
考点:空间向量的夹角与距离求解公式,空间向量的数量积运算
专题:空间向量及应用
分析:求出
+λ
与
的坐标,利用向量夹角公式即可得出.
| OA |
| OB |
| OB |
解答:
解:A(1,0,0),B(0,-1,1),
=
+λ
=(1,-λ,λ),
=
=(0,-1,1).
•
=0+λ+λ=2λ,|
|=
,|
|=
.
∴cos<
,
>=
=
.解得λ=
.
故选:B.
| a |
| OA |
| OB |
| b |
| OB |
| a |
| b |
| a |
| 1+2λ2 |
| b |
| 2 |
∴cos<
| a |
| b |
| 2λ | ||||
|
| 1 |
| 2 |
| ||
| 6 |
故选:B.
点评:本题考查了向量的数量积运算、向量夹角公式.属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
方程(
)x+x-3=0的解的个数有( )
| 1 |
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
已知等差数列{an}的前5项和S5=25,且a2=3,则a8的值是( )
| A、13 | B、14 | C、15 | D、16 |
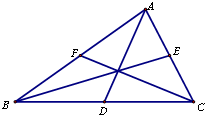 如图,△ABC中,D,E,F分别为BC,AC,AB的中点,用坐标法,证明:
如图,△ABC中,D,E,F分别为BC,AC,AB的中点,用坐标法,证明: