题目内容
已知函数y=f(x)是周期为2的周期函数,且当x∈[-1,1]时,f(x)=2|x|-1,则函数F(x)=f(x)-|lgx|的零点个数是( )
| A、10 | B、14 | C、11 | D、12 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:在坐标系中画出两个函数y1=|lgx|,y2=f(x)的图象,分析两个图象交点的个数,进而可得函数F(x)=f(x)-|lgx|的零点个数.
解答:
解:∵函数F(x)=f(x)-lg|x|的零点,
即为函数y1=lg|x|,y2=f(x)的图象的交点,
又∵函数y=f(x)是周期为2的周期函数,
且当x∈[-1,1]时,f(x)=2|x|-1,
在同一坐标系中画出两个函数y1=|lgx|,y2=f(x)的图象,如下图所示:
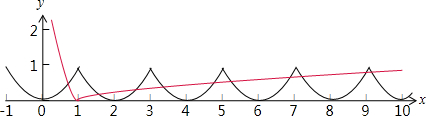
由图知,两个函数的交点共10个,
∴函数F(x)=f(x)-|lgx|的零点个数是10个
故选A.
即为函数y1=lg|x|,y2=f(x)的图象的交点,
又∵函数y=f(x)是周期为2的周期函数,
且当x∈[-1,1]时,f(x)=2|x|-1,
在同一坐标系中画出两个函数y1=|lgx|,y2=f(x)的图象,如下图所示:

由图知,两个函数的交点共10个,
∴函数F(x)=f(x)-|lgx|的零点个数是10个
故选A.
点评:本题考查函数的零点个数问题,解决的方法常用数形结合的方法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在锐角△ABC中,∠A=2∠B,则
的取值范围为( )
| c |
| b |
| A、[1,2] |
| B、[1,3] |
| C、(1,3) |
| D、(1,2) |
已知A(1,0,0),B(0,-1,1),
+λ
与
的夹角为60°,则λ的值为( )
| OA |
| OB |
| OB |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、±
|
某算法如图所示,若输入A=27,B=12,则输出的结果是( )


| A、27 | B、3 | C、0 | D、12 |
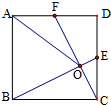 如图,在正方形ABCD中,E.F分别是CD.DA的中点,BE交CF于点O,若
如图,在正方形ABCD中,E.F分别是CD.DA的中点,BE交CF于点O,若