题目内容
已知p:|2-
|>3,q:x2-2x+1-m2>0(m>0).若p是q的必要非充分条件,求实数m的取值范围.
| x |
| 2 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:求出p,q解集,根据p是q的必要非充分条件,得出求解即可
.
|
解答:
解:∵p:|2-
|>3,
∴即x<-2,或x>10,
∵q:x2-2x+1-m2>0(m>0).
∴x<1-m或x>1+m,
∵p是q的必要非充分条件,∴
∴m≥9,
∴实数m的取值范围[9,+∞).
| x |
| 2 |
∴即x<-2,或x>10,
∵q:x2-2x+1-m2>0(m>0).
∴x<1-m或x>1+m,
∵p是q的必要非充分条件,∴
|
∴m≥9,
∴实数m的取值范围[9,+∞).
点评:本题考查了不等式的求解,充分必要条件的定义,难度不大,注意转化即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知A(1,0,0),B(0,-1,1),
+λ
与
的夹角为60°,则λ的值为( )
| OA |
| OB |
| OB |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、±
|
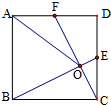 如图,在正方形ABCD中,E.F分别是CD.DA的中点,BE交CF于点O,若
如图,在正方形ABCD中,E.F分别是CD.DA的中点,BE交CF于点O,若