题目内容
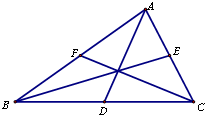 如图,△ABC中,D,E,F分别为BC,AC,AB的中点,用坐标法,证明:
如图,△ABC中,D,E,F分别为BC,AC,AB的中点,用坐标法,证明:| 3 |
| 4 |
考点:两点间的距离公式
专题:直线与圆
分析:以B为原点,BC为x轴建立平面直角坐标系,设C(a,0),A(b,c),可得D(
,0),F(
,
),E(
,
),由距离公式验证即可.
| a |
| 2 |
| b |
| 2 |
| c |
| 2 |
| a+b |
| 2 |
| c |
| 2 |
解答:
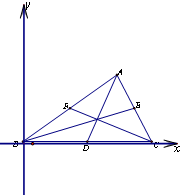 解:以B为原点,BC为x轴建立平面直角坐标系如图所示:
解:以B为原点,BC为x轴建立平面直角坐标系如图所示:
设C(a,0),A(b,c),则D(
,0),F(
,
),E(
,
),
由左边公式可得左边=
(|AB|2+|BC|2+|AC|2)=
(b2+c2+a2+a2-2ab+b2+c2)=
(a2+b2+c2-ab)
同理可得右边=|AD|2+|BE|2+|CF|2=(b-
)2+c2+
+
+(a-
)2+
=
(a2+b2+c2-ab)
∴
(|AB|2+|BC|2+|AC|2)=|AD|2+|BE|2+|CF|2
 解:以B为原点,BC为x轴建立平面直角坐标系如图所示:
解:以B为原点,BC为x轴建立平面直角坐标系如图所示:设C(a,0),A(b,c),则D(
| a |
| 2 |
| b |
| 2 |
| c |
| 2 |
| a+b |
| 2 |
| c |
| 2 |
由左边公式可得左边=
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
同理可得右边=|AD|2+|BE|2+|CF|2=(b-
| a |
| 2 |
| (a+b)2 |
| 4 |
| c2 |
| 4 |
| b |
| 2 |
| c2 |
| 4 |
| 3 |
| 2 |
∴
| 3 |
| 4 |
点评:本题考查两点间的距离公式,建系是解决问题的关键,属基础题.

练习册系列答案
相关题目
已知焦点在x轴上的双曲线
-
=1的渐近线经过点P(1,
),则该双曲线的离心率是( )
| x2 |
| m |
| y2 |
| n |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
已知A(1,0,0),B(0,-1,1),
+λ
与
的夹角为60°,则λ的值为( )
| OA |
| OB |
| OB |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、±
|