题目内容
在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且
a=2csinA
（1）确定角C的大小；
（2）若c=
，且△ABC的面积为
，求a+b的值．
| 3 |
（1）确定角C的大小；
（2）若c=
| 7 |
3
| ||
| 2 |
考点：解三角形
专题：解三角形
分析：（1）利用正弦定理把已知条件转化成角的正弦，整理可求得sinC，进而求得C．
（2）利用三角形面积求得ab的值，利用余弦定理求得a2+b2的值，最后求得a+b的值．
（2）利用三角形面积求得ab的值，利用余弦定理求得a2+b2的值，最后求得a+b的值．
解答：
解：（1）∵
a=2csinA
∴正弦定理得
sinA=2sinCsinA，
∵A锐角，
∴sinA＞0，
∴sinC=
，
又∵C锐角，
∴C=
（2）三角形ABC中，由余弦定理得c2=a2+b2-2abcosC
即7=a2+b2-ab，
又由△ABC的面积得S=
absinC=
ab
=
．
即ab=6，
∴（a+b）2=a2+b2+2ab=25
由于a+b为正，所以a+b=5．
| 3 |
∴正弦定理得
| 3 |
∵A锐角，
∴sinA＞0，
∴sinC=
| ||
| 2 |
又∵C锐角，
∴C=
| π |
| 3 |
（2）三角形ABC中，由余弦定理得c2=a2+b2-2abcosC
即7=a2+b2-ab，
又由△ABC的面积得S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
即ab=6，
∴（a+b）2=a2+b2+2ab=25
由于a+b为正，所以a+b=5．
点评：本题主要考查了正弦定理和余弦定理的运用．考查了学生对三角函数基础知识的综合运用．
练习册系列答案
相关题目
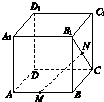如图，在正方体ABCD-A1B1C1D1中，M、N分别为AB、B1C的中点，设| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| MN |
| a |
| b |
| c |
A、x=
| ||||||
B、x=
| ||||||
C、x=
| ||||||
D、x=
|
不等式（x-1）（x-2）（x-3）＞0的解集是（ ）
| A、（1，2） |
| B、（1，2）∪（3，+∞） |
| C、（1，3） |
| D、（2，3） |
函数y=x3-3x+k有三个不同的零点，则k的取值范围是（ ）
| A、（2，+∞） |
| B、（-2，2） |
| C、（-∞，-，2） |
| D、[-2，2] |
已知a=20.1，b=ln0.1，c=sin1，则（ ）
| A、a＞b＞c |
| B、a＞c＞b |
| C、c＞a＞b |
| D、b＞a＞c |
函数f（x）=loga（ax2-x）在区间[2，4]上是增函数，则实数a的取值范围是（ ）
A、
| ||||
B、
| ||||
C、0＜a≤
| ||||
| D、a＞1 |
始边与x轴正半轴重合，终边所在直线与y轴夹角为
的角的集合是（ ）
| π |
| 6 |
A、{α|α=2kπ+
| ||||
B、{α|α=2kπ±
| ||||
C、{α|α=kπ±
| ||||
D、{α|α=kπ±
|