题目内容
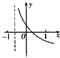 若函数f(x)=loga(x+b)(a>0,a≠1)的大致图象如图所示,则函数g(x)=ax+b的大致图象为( )
若函数f(x)=loga(x+b)(a>0,a≠1)的大致图象如图所示,则函数g(x)=ax+b的大致图象为( )A、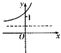 |
B、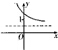 |
C、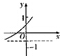 |
D、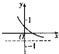 |
考点:对数函数的图像与性质,指数函数的图像变换
专题:函数的性质及应用
分析:由图象可知对数的底数满足0<a<1,且0<f(0)<1,再根据指数函数g(x)=ax+b的性质即可推得.
解答:
解:由图象可知0<a<1且0<f(0)<1,
即
即
解②得loga1<logab<logaa,
∵0<a<1∴由对数函数的单调性可知a<b<1,
结合①可得a,b满足的关系为0<a<b<1,
由指数函数的图象和性质可知,g(x)=ax+b的图象是单调递减的,且一定在x轴上方.
故选:B.
即
|
解②得loga1<logab<logaa,
∵0<a<1∴由对数函数的单调性可知a<b<1,
结合①可得a,b满足的关系为0<a<b<1,
由指数函数的图象和性质可知,g(x)=ax+b的图象是单调递减的,且一定在x轴上方.
故选:B.
点评:本小题主要考查对数函数的图象、指数函数的图象、对数函数的图象的应用、方程组的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,属于基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
设曲线y=eax-ln(x+1)在点(0,1)处的切线方程为2x-y+1=0,则a=( )
| A、0 | B、1 | C、2 | D、3 |
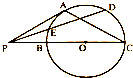 如图,P是⊙O外一点,PA是切线,割线PBC经过圆心O,且PB=
如图,P是⊙O外一点,PA是切线,割线PBC经过圆心O,且PB=