题目内容
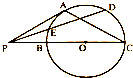 如图,P是⊙O外一点,PA是切线,割线PBC经过圆心O,且PB=
如图,P是⊙O外一点,PA是切线,割线PBC经过圆心O,且PB=| 1 |
| 2 |
(Ⅰ)求证:PA=AC;
(Ⅱ)若点D是弧AC的中点,PD与⊙O交于另一点E,PB=1,求PE的长.
考点:与圆有关的比例线段
专题:立体几何
分析:(I)利用切割线定理可得PA2=PB•PC,即可得出;
(II)连接OD,CD,利用D为
的中点,可得∠COD=
∠AOC=60°,PB=1,PC=3,CD=1.由余弦定理得PD2=PC2+CD2-2PC•CDcos60°可得PD=
,再由切割线定理可得PA2=PE•PD,即可得出.
(II)连接OD,CD,利用D为
 |
| AC |
| 1 |
| 2 |
| 7 |
解答:
(Ⅰ)证明:设BC=2R,则PB=R,PC=3R,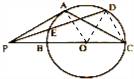
∵PA为切线,由切割线定理得,PA2=PB•PC=3R2,
∴PA=
R.
连接OA,PA⊥OA,
∴∠POA=60°.∠AOC=120°.
∴AC=
R,∴PA=AC.
(Ⅱ) 解:连接OD,CD,
∵D为
的中点,
∴∠COD=
∠AOC=60°,
而OC=OD,∠PCD=60°,
∵PB=1,
∴PC=3,CD=1,
由余弦定理得PD2=PC2+CD2-2PC•CDcos60°=32+12-2×3×
=7,
∴PD=
,
再由切割线定理得,PA2=PE•PD,
∴3=
PE.
∴PE=
.

∵PA为切线,由切割线定理得,PA2=PB•PC=3R2,
∴PA=
| 3 |
连接OA,PA⊥OA,
∴∠POA=60°.∠AOC=120°.
∴AC=
| 3 |
(Ⅱ) 解:连接OD,CD,
∵D为
 |
| AC |
∴∠COD=
| 1 |
| 2 |
而OC=OD,∠PCD=60°,
∵PB=1,
∴PC=3,CD=1,
由余弦定理得PD2=PC2+CD2-2PC•CDcos60°=32+12-2×3×
| 1 |
| 2 |
∴PD=
| 7 |
再由切割线定理得,PA2=PE•PD,
∴3=
| 7 |
∴PE=
3
| ||
| 7 |
点评:本题考查了切割线定理、余弦定理、圆的切线的性质、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
变量x,y满足约束条件
时,x-2y+m≤0恒成立,则实数m的取值范围为( )
|
| A、[0,+∞) |
| B、[1,+∞) |
| C、(-∞,3] |
| D、(-∞,0] |
一个空间几何体的三视图如图所示,则该几何体的体积为( )
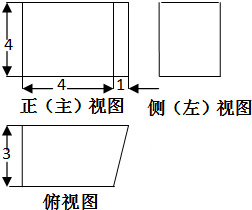

| A、12 | B、18 | C、27 | D、54 |
原命题:“设a、b、c∈R,若ac2>bc2则a>b”和它的逆命题、否命题、逆否命题这四个命题中,真命题共有( )
| A、1个 | B、2个 | C、3个 | D、0个 |
圆 C1:(x+2)2+(y-2)2=4和圆C2:(x-2)2+(y-5)2=16的位置关系是( )
| A、外离 | B、相交 | C、内切 | D、外切 |
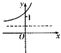
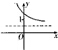
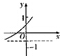
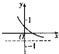
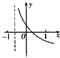 若函数f(x)=loga(x+b)(a>0,a≠1)的大致图象如图所示,则函数g(x)=ax+b的大致图象为( )
若函数f(x)=loga(x+b)(a>0,a≠1)的大致图象如图所示,则函数g(x)=ax+b的大致图象为( )