题目内容
设曲线y=eax-ln(x+1)在点(0,1)处的切线方程为2x-y+1=0,则a=( )
| A、0 | B、1 | C、2 | D、3 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:根据导数的几何意义求出函数f(x)在x=0处的导数,从而求出切线的斜率,再根据曲线y=eax-ln(x+1)在点(0,1)处的切线方程为2x-y+1=0,建立等式关系,解之即可.
解答:
解:∵y=eax-ln(x+1),∴y′=aeax-
∴x=0时,切线的斜率为a-1
∵曲线y=eax-ln(x+1)在点(0,1)处的切线方程为2x-y+1=0,
∴a-1=2,即a=3.
故选:D.
| 1 |
| x+1 |
∴x=0时,切线的斜率为a-1
∵曲线y=eax-ln(x+1)在点(0,1)处的切线方程为2x-y+1=0,
∴a-1=2,即a=3.
故选:D.
点评:本题主要考查了利用导数研究曲线上某点切线方程,考查学生的计算能力,属于基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
下列命题错误的是( )
| A、命题“若p则q”与命题“若¬q,则¬p”互为逆否命题 | ||||||||||||
| B、命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0” | ||||||||||||
C、“
| ||||||||||||
| D、“若am2<bm2,则a<b”的逆命题为真 |
原命题:“设a、b、c∈R,若ac2>bc2则a>b”和它的逆命题、否命题、逆否命题这四个命题中,真命题共有( )
| A、1个 | B、2个 | C、3个 | D、0个 |
底面为正三角形且侧棱与底面垂直的三棱柱称为正三棱柱,则棱长均为a的正三棱柱外接球的表面积为( )
A、
| ||
B、
| ||
C、
| ||
| D、πa2 |
若函数f(x)=loga(x+1)的定义域和值域都为[0,1],则a的值为( )
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
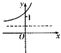
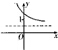
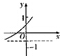
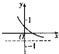
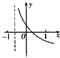 若函数f(x)=loga(x+b)(a>0,a≠1)的大致图象如图所示,则函数g(x)=ax+b的大致图象为( )
若函数f(x)=loga(x+b)(a>0,a≠1)的大致图象如图所示,则函数g(x)=ax+b的大致图象为( )