题目内容
已知数列{an}满足a1=2，an+1=
+1．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=an+an+1-2，证明
+
+…+
＜
．
| an2-2an+2 |
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=an+an+1-2，证明
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| n+1 |
考点：数列与不等式的综合
专题：综合题,等差数列与等比数列
分析：（Ⅰ）证明{（an-1）2}是首项为1，公差为1的等差数列，即可求数列{an}的通项公式；
（Ⅱ）由（Ⅰ）知，bn=an+an+1-2=
+
，可得
+
+…+
=
-1+
-
+…+
-
=
-1，即可证明结论．
（Ⅱ）由（Ⅰ）知，bn=an+an+1-2=
| n+1 |
| n |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 2 |
| 3 |
| 2 |
| n+1 |
| n |
| n+1 |
解答：
（Ⅰ）解：∵an+1=
+1，
∴（an+1-1）2-（an-1）2=1，
又（a1-1）2=1
∴{（an-1）2}是首项为1，公差为1的等差数列…（4分）
∴（an-1）2=n
∴an-1=
，∴an=
+1…（7分）
（Ⅱ） 由（Ⅰ）知，bn=an+an+1-2=
+
∴
+
+…+
=
-1+
-
+…+
-
=
-1
于是，
+
+…+
＜
．…（12分）
| an2-2an+2 |
∴（an+1-1）2-（an-1）2=1，
又（a1-1）2=1
∴{（an-1）2}是首项为1，公差为1的等差数列…（4分）
∴（an-1）2=n
∴an-1=
| n |
| n |
（Ⅱ） 由（Ⅰ）知，bn=an+an+1-2=
| n+1 |
| n |
∴
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 2 |
| 3 |
| 2 |
| n+1 |
| n |
=
| n+1 |
于是，
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| n+1 |
点评：本题考查数列与不等式的综合，考查数列的通项，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
设l，m是两条不同的直线，α是一个平面，则下列命题正确的是（ ）
| A、若l∥α，m⊥α，则l⊥m |
| B、若l⊥m，m∥α则l⊥α |
| C、若l⊥m，m⊥α，则l∥α |
| D、若l∥α，m∥α则l∥m |
变量x，y满足约束条件
时，x-2y+m≤0恒成立，则实数m的取值范围为（ ）
|
| A、[0，+∞） |
| B、[1，+∞） |
| C、（-∞，3] |
| D、（-∞，0] |
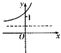
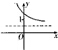
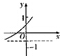
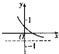
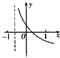若函数f（x）=loga（x+b）（a＞0，a≠1）的大致图象如图所示，则函数g（x）=ax+b的大致图象为（ ）
若函数f（x）=loga（x+1）的定义域和值域都为[0，1]，则a的值为（ ）
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|