题目内容
过抛物线y2=2px(p>0)的焦点的一条直线与抛物线相交,交点为A、B.过AB的中点M作x轴的平行线交抛物线的准线于点C.求证:AC⊥BC.
考点:直线与圆锥曲线的关系
专题:向量与圆锥曲线
分析:证AC⊥BC,即证
⊥
,即证
•
=0,设出点的坐标,将直线方程与双曲线方程联立,结合韦达定理,即可证明.
| AC |
| BC |
| AC |
| BC |
解答:
解:如图:
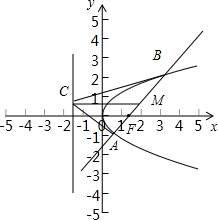
①当直线AB的斜率不存在时,F(
,0),直线AB方程为x=
,则C(-
,0),设A(x1,y1),B(x2,y2),由题意得
消去x得y2=p2,∴y1=-p,y2=p,A(
,-P),B(
,P),∴
=(-p,p),
=(-p,-p),
∴
•
=0,∴AC⊥BC.
②当当直线AB的斜率存在时,F(
,0),设直线AB方程为y=k(x-
),设A(x1,y1),B(x2,y2),则C(-
,
),由题意得
消去y得,k2x2-(k2p+2p)x+
=0,∴x1+x2=
,x1x2=
,y1+y2=k(x1+x2)-kp=
,y1y2=-p2,
∴
=(-
-x1,
),
=(-
-x2,
),
∴
•
=(
+x1)(
+x2)-
=
+
(x1+x2)+x1x2-
=0
∴AC⊥BC.
综上所述;AC⊥BC.

①当直线AB的斜率不存在时,F(
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
|
| P |
| 2 |
| P |
| 2 |
| AC |
| BC |
∴
| AC |
| BC |
②当当直线AB的斜率存在时,F(
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| y1+y2 |
| 2 |
|
| k2p2 |
| 4 |
| k2p+2p |
| k2 |
| p2 |
| 4 |
| 2p |
| k |
∴
| AC |
| p |
| 2 |
| y2-y1 |
| 2 |
| BC |
| p |
| 2 |
| y1-y2 |
| 2 |
∴
| AC |
| AB |
| p |
| 2 |
| p |
| 2 |
| (y1-y2)2 |
| 4 |
| p2 |
| 4 |
| p |
| 2 |
| (y1+y2)2-4y1y2 |
| 4 |
∴AC⊥BC.
综上所述;AC⊥BC.
点评:本题主要考查直线与双曲线的位置关系及向量垂直的充要条件等知识,考查学生分析问题、解决问题的能力及等价转化能力、运算求解能力,属于难题.

练习册系列答案
相关题目
已知{an}为等差数列,0<d<1,a5≠
,sin2a3+2sina5cosa5=sin2a7,Sn为数列{an}的前n项和,若Sn≥S10对一切n∈N*都成立,则首项a1的取值范围是( )
| kπ |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、(-
| ||||
D、[-
|
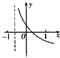 若函数f(x)=loga(x+b)(a>0,a≠1)的大致图象如图所示,则函数g(x)=ax+b的大致图象为( )
若函数f(x)=loga(x+b)(a>0,a≠1)的大致图象如图所示,则函数g(x)=ax+b的大致图象为( )