题目内容
设f(x)=
+xlnx,g(x)=x3-x2-3.
(1)当x∈[0,2]时,求g(x)的最大值和最小值;
(2)如果对任意的s,t∈[
,2],都有f(s)≥g(t)成立,求实数a的取值范围.
| a |
| x |
(1)当x∈[0,2]时,求g(x)的最大值和最小值;
(2)如果对任意的s,t∈[
| 1 |
| 2 |
考点:利用导数求闭区间上函数的最值
专题:计算题,导数的综合应用
分析:(1)求导,由导数确定函数在[0,2]上的单调性,由单调性求最值;
(2)由(1)知,在区间[
,2]上,gmax(x)=g(2)=1;从而原问题等价于当x∈[
,2]时,f(x)=
+xlnx≥1恒成立,用分离系数法可得a≥x-x2lnx恒成立,从而转化为求函数h(x)=x-x2lnx在区间[
,2]上的最大值,利用求导求单调性,再求最值即可.
(2)由(1)知,在区间[
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| x |
| 1 |
| 2 |
解答:
解:(1)对于函数g(x)=x3-x2-3,x∈[0,2],
g′(x)=3x2-2x,
令g′(x)=0,得x=0或x=
;
当x变化时,g(x)、g′(x)变化情况如下表:
由上表可知:gmin(x)=-
,gmax(x)=g(2)=1,
(2)由(1)知,在区间[
,2]上,gmax(x)=g(2)=1.
则原问题等价于当x∈[
,2]时,f(x)=
+xlnx≥1恒成立,
等价于a≥x-x2lnx恒成立,
记h(x)=x-x2lnx,h′(x)=1-2xlnx-x,h′(1)=0;
记m(x)=1-2xlnx-x,m′(x)=-3-2lnx,
∵x∈[
,2],
∴m′(x)=-3-2lnx<0,
∴m(x)=1-2xlnx-x在[
,2]上递减,
且当x∈[
,1)时,h′(x)>0,x∈(1,2]时,h′(x)<0,
即函数h(x)=x-x2lnx在区间[
,1)上递增,在区间(1,2]上递减,
∴hmax(x)=h(1)=1,
∴a≥1.
g′(x)=3x2-2x,
令g′(x)=0,得x=0或x=
| 2 |
| 3 |
当x变化时,g(x)、g′(x)变化情况如下表:
| x | 0 | (0,
|
| (
| 2 | ||||||
| g′(x) | 0 | - | 0 | + | + | ||||||
| g(x) | -3 | 递减 | 极(最)小值-
| 递增 | 1 |
| 85 |
| 27 |
(2)由(1)知,在区间[
| 1 |
| 2 |
则原问题等价于当x∈[
| 1 |
| 2 |
| a |
| x |
等价于a≥x-x2lnx恒成立,
记h(x)=x-x2lnx,h′(x)=1-2xlnx-x,h′(1)=0;
记m(x)=1-2xlnx-x,m′(x)=-3-2lnx,
∵x∈[
| 1 |
| 2 |
∴m′(x)=-3-2lnx<0,
∴m(x)=1-2xlnx-x在[
| 1 |
| 2 |
且当x∈[
| 1 |
| 2 |
即函数h(x)=x-x2lnx在区间[
| 1 |
| 2 |
∴hmax(x)=h(1)=1,
∴a≥1.
点评:本题考查了导数的综合应用,同时考查了恒成立问题的处理方法,化简比较困难,属于难题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
已知{an}为等差数列,0<d<1,a5≠
,sin2a3+2sina5cosa5=sin2a7,Sn为数列{an}的前n项和,若Sn≥S10对一切n∈N*都成立,则首项a1的取值范围是( )
| kπ |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、(-
| ||||
D、[-
|
满足“对定义域内任意实数x,y,都有f(x•y)=f(x)+f(y)”的单调递减函数是( )
| A、y=log2x |
| B、y=log0.3x |
| C、y=3x |
| D、y=0.1x |
设l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )
| A、若l∥α,m⊥α,则l⊥m |
| B、若l⊥m,m∥α则l⊥α |
| C、若l⊥m,m⊥α,则l∥α |
| D、若l∥α,m∥α则l∥m |
底面为正三角形且侧棱与底面垂直的三棱柱称为正三棱柱,则棱长均为a的正三棱柱外接球的表面积为( )
A、
| ||
B、
| ||
C、
| ||
| D、πa2 |
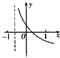 若函数f(x)=loga(x+b)(a>0,a≠1)的大致图象如图所示,则函数g(x)=ax+b的大致图象为( )
若函数f(x)=loga(x+b)(a>0,a≠1)的大致图象如图所示,则函数g(x)=ax+b的大致图象为( )