题目内容
已知圆x2+y2=4,直线l:y=x+b,当圆上由2个点到直线l的距离为1,则b的取值范围为 .
考点:直线与圆的位置关系
专题:计算题,直线与圆
分析:由题意可得圆心(0,0)到直线l:y=x+b的距离d满足1<d<3.根据点到直线的距离公式求出d,再解绝对值不等式求得实数b的取值范围.
解答:
解:由题意可得圆心(0,0)到直线l:y=x+b的距离d满足1<d<3,
由于d=
,∴1<
<3,即
<|b|<3
,
解得b∈(-3
,-
)∪(
,3
),
故答案为:(-3
,-
)∪(
,3
).
由于d=
| |b| | ||
|
| |b| | ||
|
| 2 |
| 2 |
解得b∈(-3
| 2 |
| 2 |
| 2 |
| 2 |
故答案为:(-3
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式,绝对值不等式的解法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
底面为正三角形且侧棱与底面垂直的三棱柱称为正三棱柱,则棱长均为a的正三棱柱外接球的表面积为( )
A、
| ||
B、
| ||
C、
| ||
| D、πa2 |
若函数f(x)=loga(x+1)的定义域和值域都为[0,1],则a的值为( )
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
圆 C1:(x+2)2+(y-2)2=4和圆C2:(x-2)2+(y-5)2=16的位置关系是( )
| A、外离 | B、相交 | C、内切 | D、外切 |
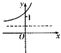
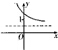
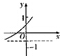
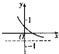
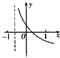 若函数f(x)=loga(x+b)(a>0,a≠1)的大致图象如图所示,则函数g(x)=ax+b的大致图象为( )
若函数f(x)=loga(x+b)(a>0,a≠1)的大致图象如图所示,则函数g(x)=ax+b的大致图象为( )