题目内容
4张卡片的正、反两面分别写有数字0,1;2,3;4,5;6,7,将这4张卡片排成一排,可构成 个不同的四位偶数.
考点:计数原理的应用
专题:排列组合
分析:把四位偶数分为两类:个位位是0,个位不是0,分别求出每一类的偶数的个数,相加即得所求.
解答:
解:分两种情况:
个位是0时,则组成前三位数时没有限制,排列
,确定每一张哪一面朝上各有2种,有
×23=48个,
个位是不是0时,当1在千位上时,个位只能从2,4,6中选一个,百位和十位再剩下的两张排列,确定每一张哪一面朝上各有2种,有
•
×22=24个,
个位是不是0时,当千上不是1时,个位只能从2,4,6中选一个有3种,再确定千位,有
=4种,再排百位和十位,有
×22=8种,则偶数的个数为3×4×8=96个,
根据分类计数原理得,48+24+96=168.
故答案为:168.
个位是0时,则组成前三位数时没有限制,排列
| A | 3 3 |
| A | 3 3 |
个位是不是0时,当1在千位上时,个位只能从2,4,6中选一个,百位和十位再剩下的两张排列,确定每一张哪一面朝上各有2种,有
| C | 1 3 |
| A | 2 2 |
个位是不是0时,当千上不是1时,个位只能从2,4,6中选一个有3种,再确定千位,有
| C | 1 2 |
| •A | 2 2 |
| A | 2 2 |
根据分类计数原理得,48+24+96=168.
故答案为:168.
点评:本题主要考查排列、组合以及简单计数原理的应用,体现了分类讨论的数学思想.

练习册系列答案
相关题目
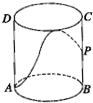 如图,有一圆柱形的开口容器(下表面密封),其轴截面是边长为4的正方形,P是BC中点,现有一只蚂蚁位于外壁外处,内壁P处有一米粒,则这只蚂蚁取得米粒所需经过的最短路程为
如图,有一圆柱形的开口容器(下表面密封),其轴截面是边长为4的正方形,P是BC中点,现有一只蚂蚁位于外壁外处,内壁P处有一米粒,则这只蚂蚁取得米粒所需经过的最短路程为